HOW TO SKETCH SQUARE ROOT FUNCTION

Sketch the graphs of the following functions.

Problem 1 :

y  =  x√(4-x)

Solution :

Domain and range :

Possible values of x are (-∞, 3) ==>  Domain

y values are (-∞, 4) ==>  Range

Intercepts :

To find x intercept, put y  =  0

  x√(4-x)  =  0

x intercepts are 0 and 4. 

y-intercept :

Put x  =  0

y  =  0

Critical points :

f(x)  =  x√(4-x)

f'(x)  =  x(1/2√(4-x))(-1) + √(4-x) (1)

f'(x)  =  -x/2√(4-x) + √(4-x)

f'(x)  =  [-x+2(4-x)]/2√(4-x)

f'(x)  =  (-x+8-2x)/2√(4-x)

f'(x)  =  (8-3x)/2√(4-x)

f'(x)  =  0

(8-3x)/2√(4-x)  =  0

3x  =  8

x  =  8/3

Plotting these points on the number line and dividing into intervals, we get (-∞, 8/3) and (8/3, ∞).

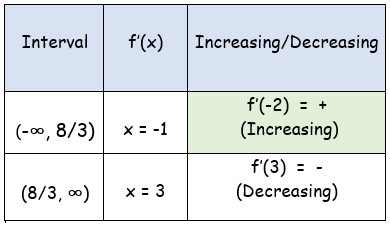
Local extrema :

f'(x)  =  (8-3x)/2√(4-x)

u  =  8-3x and v  =  2√(4-x)

u'  =  -3 and v'  =  -1/√(4-x)

f''(x)  =  [2√(4-x)(-3)-(8-3x)(-1/√(4-x))] /4(4-x)

f''(x)  =  (3x-16)/4(4-x)√(4-x)

f''(8/3)  =  - < 0 (Maximum)

Maximum value at x  =  8/3 :

y  =  x√(4-x)

y  =  (8/3)√(4-(8/3))

y  =  (8/3)√(4/3)

y  =  16/3√3

So, the maximum point is (8/3, 16/3√3).

Intervals of concavity :

f''(x)  =  (3x-16)/4(4-x)√(4-x)

f''(x)  =  0

3x-16  =  0

x  =  16/3

It is not in the domain, so it has no real value on.

Point of inflection :

There is no point of inflection.

Asymptotes :

As x ->∞, y -> ±∞

Apart from the stuff given above, if you need any other stuff in math, please use our google custom search here.

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.