HOW TO SOLVE AN EQUATION

An equation is like a weighing balance with equal weights on both of its pans, in which case the arm of the balance are exactly horizontal.

If we add the same weights to both the pans, the arms remains horizontal. In the same way, if we remove the same weights from both the pans, then also the arm remains horizontal. We use the same principle for solving an equation.

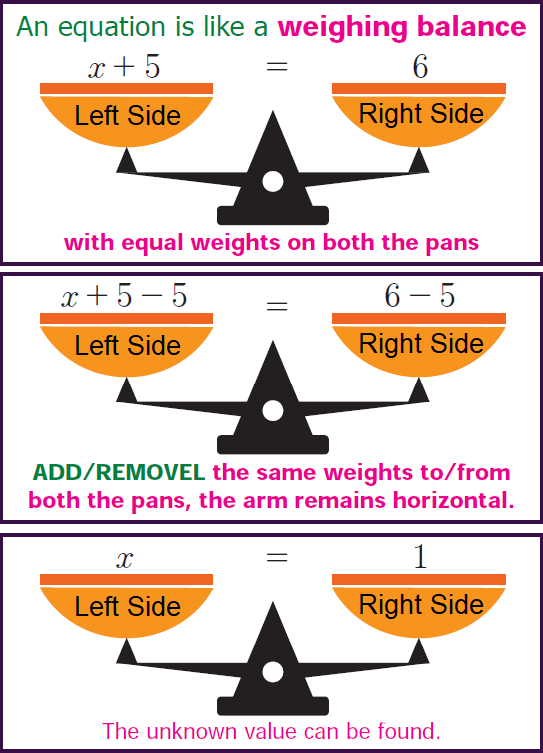
We use the following principles to separate the variables and constants thereby solving an equation.

Try This

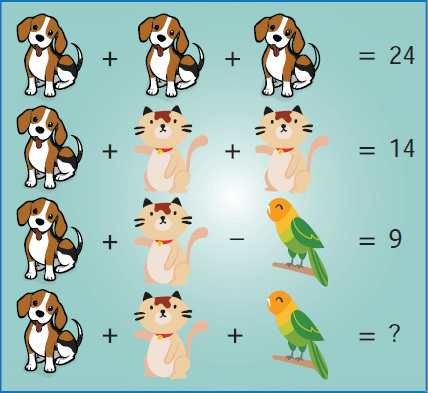
If the dogs, cats and parrots in the picture above represent unknowns, find them. Substitute each of the values so obtained in the equations and verify the answers.

Solved Examples

Examples 1-7 : Solve for x.

Example 1 :

x + 5 = 7

Solution :

x + 5 = 7

Subtract 5 from both sides.

(x + 5) - 5 = 7 - 5

x + 5 - 5 = 2

x + 0 = 2

x = 2

Example 2 :

x - 2 = 3

Solution :

x - 2 = 3

Add 2 to both sides.

(x - 2) + 2 = 3 + 2

x - 2 + 2 = 5

x + 0 = 5

x = 5

Example 3 :

7x = 21

Solution :

7x = 21

Divide both sides by 7.

⁷ˣ⁄₇ = ²¹⁄₇

x = 3

Example 4 :

ˣ⁄₂ = -6

Solution :

ˣ⁄₂ = -6

Multiply both sides by 2.

2(ˣ⁄₂) = 2(-6)

x = -12

Example 5 :

3x + 2 = 11

Solution :

3x + 2 = 11

Subtract 2 from both sides.

(3x + 2) - 2 = 11 - 2

3x + 2 - 2 = 9

3x + 0 = 9

3x = 9

³ˣ⁄₃ = ⁹⁄₃

x = 3

Example 6 :

³ˣ⁄₂ = 6

Solution :

³ˣ⁄₂ = 6

Multiply both sides by 2.

2(³ˣ⁄₂) = 2(6)

3x = 12

³ˣ⁄₃ = ¹²⁄₃

x = 4

Example 7 :

⁽³ˣ ⁺ ²⁾⁄₅ = 4

Solution :

⁽³ˣ ⁺ ²⁾⁄₅ = 4

Multiply both sides by 5.

5[⁽³ˣ ⁺ ²⁾⁄₅] = 5(4)

3x + 2 = 20

Subtract 2 from both sides.

(3x + 2) - 2 = 20 - 2

3x + 2 - 2 = 18

3x + 0 = 18

3x = 18

Divide both sides by 3.

³ˣ⁄₃ = ¹⁸⁄₃

x = 6

Example 8 :

Find two consecutive natural numbers whose sum is 75.

Solution :

The numbers are natural and consecutive. Let the numbers be x and x + 1.

From the information given,

x + (x + 1) = 75

x + x + 1 = 75

2x + 1 = 75

Subtract 1 from both sides.

(2x + 1) - 1 = 75 - 1

2x + 1 - 1 = 74

2x = 74

Divide both sides by 2.

²ˣ⁄₂ = ⁷⁴⁄₂

x = 37

x + 1 = 38

Therefore, the required numbers are 37 and 38.

Example 9 :

In an examination, a student scores 4 marks for every correct answer and loses one mark for every wrong answer. If he answers 60 questions in all and gets 130 marks, find the number of questions he answered correctly.

Solution :

Let the number of correct answers be x.

Thus the number of wrong answers is (60 - x).

From the information given,

4x - 1(60 - x) = 130

4x - 60 + x = 130

5x - 60 = 130

Add 60 to both sides.

(5x - 60) + 60 = 130 + 60

5x - 60 + 60 = 190

5x + 0 = 190

5x = 190

Divide both sides by 5.

⁵ˣ⁄₅ = ¹⁹⁰⁄₅

x = 38

Therefore, the number of correct answer is 38.

Example 10 :

A school bus starts with full strength of 60 students. It drops some students at the first bus stop. At the second bus stop, twice the number of students get down from the bus. 6 students get down at the third bus stop and the number of students remaining in the bus is only 3. How many students got down at the first stop?

Solution :

Since we do not know the number of students who get down at the first stop, let us take the number as x. The number of students get down at the second bus stop is 2x.

From the inforamtion given,

x + 2x + 6 + 3 = 60

3x + 9 = 60

Subtract 9 from both sides.

(3x + 9) - 9 = 60 - 9

3x + 9 - 9 = 51

3x = 51

Divide both sides by 3.

³ˣ⁄₃ = ⁵¹⁄₃

x = 17

Therefore, the number of students got down in the first bus stop is 17.

Try This

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.