QUADRATICS WORD PROBLEMS WITH ANSWERS

To see from questions 1 to 3, please visit the page "Solving Word Problems Involving Quadratic Equations"

To find questions from 4 to 6, please visit the page "Quadratics Word Problems with Answers"

Question 7 :

Music is been played in two opposite galleries with certain group of people. In the first gallery a group of 4 singers were singing and in the second gallery 9 singers were singing. The two galleries are separated by the distance of 70 m. Where should a person stand for hearing the same intensity of the singers voice? (Hint: The ratio of the sound intensity is equal to the square of the ratio of their corresponding distances).

Solution :

The ratio of the sound intensity is equal to the square of the ratio of their corresponding distances

let "d" is the distance from galley of 4 singers 

The distance from gallery of 9 singers = 70 - d

4x/d² = 9x/(70-d)²

4(70-d)² =  9d²

By taking square root on both sides, we get

2(70 -d) = 3d

140 - 2d = 3d

140 = 5d

d = 28 

28 m from Gallery of 4 singers

42 m from gallery of 9  singers

Question 8 :

There is a square field whose side is 10 m. A square flower bed is prepared in its centre leaving a gravel path all round the flower bed. The total cost of laying the flower bed and gravelling the path at ₹3 and ₹4 per square metre respectively is ₹364. Find the width of the gravel path.

Solution :

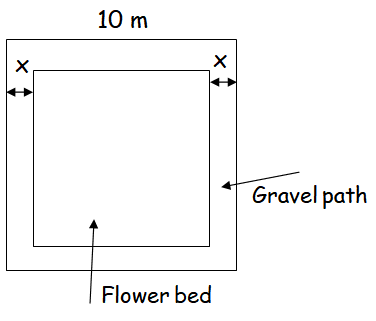
Let "x" be the width of the gravel.

Side length of square   =  10

Area of square field  =  10 (10)  =  400

Side length of flower bed  =  10 - 2x

Area of flower bed  =  (10 - 2x)² 

  =  100 + 4x² - 40x 

Cost of laying the flower bed  =  3(100 + 4x² - 40x)

=  300 + 12x² - 120x  -----(1)

Area of gravel path  =  100 - (100 + 4x² - 40x)

=  40x - 4x²

Cost of laying the gravel path  =  4(40x - 4x²)

=  160x - 16x²  -----(2)

(1) + (2)

160x - 16x² + 300 + 12x² - 120x  =  364

-4x² + 40x + 300 - 364  =  0

-4x² + 40x - 64  =  0

Divide the entire equation by (-4), we get

x² - 10x + 16 =  0

(x - 2)(x - 8)  =  0

x  =  2 and x = 8

Hence, 2 m is the width of gravel path.

Question 9 :

Two women together took 100 eggs to a market, one had more than the other. Both sold them for the same sum of money. The first then said to the second: “If I had your eggs, I would have earned ₹15”, to which the second replied: “If I had your eggs, I would have earned ₹ 6 ⅔”. How many eggs did each had in the beginning?

Solution :

Let "x" be the number of eggs in the 1^st person.   

Then the number of eggs in the 2^nd person  =  100 - x.

Cost price of each egg for the first person is not equal to the cost price of each egg for the second person.

Let "p" and "q" be the cost price of each egg for the 1^st and 2^nd persons respectively.

Given : Both sold them for the same sum of money.

So, we have

px  =  q(100 - x)

p/q  =  (100 - x) / x -----(1)

Given : The first then said to the second: “If I had your eggs, I would have earned ₹15”, to which the second replied: “If I had your eggs, I would have earned ₹ 6⅔”. 

So, we have

p(100 - x)  =  15 -----(2)

qx  =  6⅔

qx  =  20/3 -----(3)

(2) ÷ (3) : 

p(100 - x) ÷ qx  =  15 ÷ (20/3)

p(100 - x) / qx  =  15 ⋅ 3/20

p(100 - x) / qx  =  3 ⋅ 3/4

p(100 - x) / qx  =  9/4

p/q  =  9x / 4(100 - x) -----(4)

From (1) and (4), we get

9x / 4(100 - x)  =  (100 - x) / x

9x²  =  4(100 - x)²

(3x)²  =  [2(100 - x)]²

Take square root on both sides.

3x  =  2(100 - x)

3x  =  200 - 2x

5x  =  200

x  =  40

100 - x  =  100 - 40

100 - x  =  60

Number of eggs had by the first person  =  40

Number of eggs had by the second person  =  60

Question 10 :

The hypotenuse of a right angled triangle is 25 cm and its perimeter 56 cm. Find the length of the smallest side.

Solution :

Length of hypotenuse side  =  25 cm

Perimeter of the triangle  =  56

sum of lengths of all sides  =  56 - 25

  =  31

If "x" be the side length of one side, then "31 - x" will be the side length of other side.

In a right triangle,

(Hypotenuse side)² =  Sum of squares of other two sides

25²  =  x² + (31 - x)²

625  = x² + 961 + x² - 62x

2x² - 62x + 961 - 625  =  0

2x² - 62x + 336  =  0

x² - 31x + 168  =  0

(x -24)(x - 7)  =  0

x  =  24 and x = 7

31 - x  =  31 - 7  =  24

The sides of the triangle are 7, 24 and 25

Hence, the smallest side measures 7 cm.

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.