HOW TO SOLVE TIME AND DISTANCE PROBLEMS

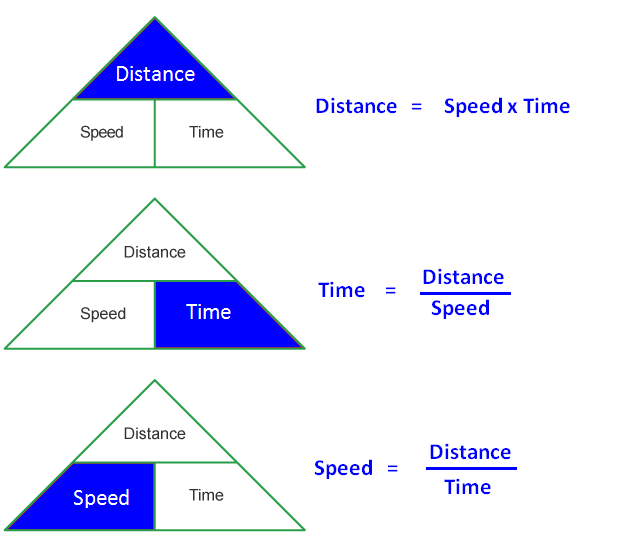
Formulas

Time, Speed and Distance Shortcuts

Shortcut 1 :

Let the speed be given in km per hour. 

If we want to convert it in to meter per second, then we have to multiply the given speed by 5/18.

Example :

108 km/hr  =  108 ⋅ 5/18 meters/sec

108 km/hr  =  30 meters/sec

Shortcut 2 :

Let the speed be given in meter per sec. 

If we want to convert it in to km per hour, then we have to multiply the given speed by 18/5.

Example :

35 meters/sec  =  35 ⋅ 18/5 kms/hr

35 meters/sec  =  126 kms/hr

Shortcut 3 :

Let the speeds of two vehicles be in the ratio a : b.

Then, the ratio of the time taken by the two vehicles to cover the same distance is b : a.

Example :

Let the ratio of speeds of two vehicles be 3 : 4.

Then, the ratio of the time taken by the two vehicles to cover the same distance is 4 : 3.

Shortcut 4 :

Let the speeds of two vehicles be in the ratio a : b.

Then, the ratio of distances covered by the two vehicles in the same amount of time is also a : b.

Example :

Let the ratio of speeds of two vehicles be 3 : 4. Each vehicle is given one hour time. Then, the distance covered by the two vehicles will be in the ratio 3 : 4.  

Shortcut 5 :

Let A be twice as fast as B.

Then, the ratio of distances covered by A and B in the same amount of time will be 2 : 1.

Example :

Let A be twice as fast as B and each given 1 hour time.  If A covers 40 miles of distance, then B will cover 20 miles of distance.

Shortcut 6 :

Let the speed of a vehicle be increased or decreased in the ratio a : b. 

Then the new speed  is

=  “b” of the original speed / a

More clearly, new speed  is

=  (“b” ⋅ original speed) / a

Example :

Michael travels at a speed of 63 miles per hour. If he reduces his speed in the ratio 9 : 8, find his new speed.

New speed  =  (8 ⋅ 63) / 9

New speed  =  56 miles per hour

Shortcut 7 :

A vehicle covers a particular distance at a speed “a” miles per hour and comes back to its original position at a speed of “b” miles per hour.

Then the average speed for the total distance covered is

= 2ab / (a + b) miles hour

Important Condition :

The distance covered in “a” miles per hour and the distance covered in “b” miles per hour must be same.

Example :

Kevin covers 300 miles at the speed 45 mph and travels another 300 miles at the speed of 55 mph. Find the average speed for the whole journey.

Average speed for the whole journey is

=  (2 ⋅ 45 ⋅ 55) / (45 + 55)

=  4950 / 90

=  55 miles per hour  

Solving Time and Distance Problem

Question :

A person covers a certain distance at a certain speed. If he increases his speed by 33⅓%, he takes 15 minutes less to cover the same distance. Find the time taken by him initially to cover the distance at the original speed.

Solution :

Step 1 :

Let us understand the given information. There are two information given in the question. 

1. A person covers a certain distance at a certain speed.

2. If the speed is increased by 33⅓%, he takes 15 minutes less to cover the same distance. 

Step 2 :

Target of the question :

Time taken by him initially to cover the distance at the original speed.

Step 3 :

Let 100% be the original speed.

If the speed is increased by 33⅓%, then the speed after increment is 133⅓%.

Step 4 :

Ratio of the speeds   =  (100 %) : (133⅓%)

                                   =  100 : 400/3

Ratio of the speeds  =  1 : 4/3

Step 5 :

If the ratio of the speeds is 1 : 4/3, then the ratio of time taken would be

1 : 3/4

Step 6 :

When the speed is increased by 33⅓%, 3/4 of the original time is enough to cover the same distance.

That is, when the speed is increased by 33⅓%, 1/4 of the original time will be decreased -------(1)

The question says that when speed is increased by 33 1/3%, time is decreased by 15 minutes -------(2)

Let "x" be the original time.

Comparing the statements (1) & (2), we get

1/4 of "x"  = 15 minutes

(1/4)x = 15

Multiply each side by 4.

x = 60

Original time  =  60 minutes

So, time taken by him initially is 60 minutes or 1 hour

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.