HOW TO TEST IF THE GIVEN FUNCTION HAS REMOVABLE DISCONTINUITY

The function f(x) is defined at all points of the real line except x = 0. That is, f(0) is undefined, but lim x -> 0 sin x/x  =  1. If we redefine the function f(x) as 

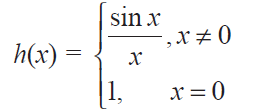
h is defined at all points of the real line including x = 0. Moreover, h is continuous at x = 0 since 

lim _{x -> 0} h(x)  = lim _{x -> 0} (sin x / x)   =  1  =  h(0)

Note that h(x) = f(x) for all x ≠ 0. Even though the original function f(x) fails to be continuous at x = 0, the redefined function became continuous at 0.

That is, we could remove the discontinuity by redefining the function. Such discontinuous points are called removable  discontinuities. This example leads us to have the following.

Definition of removable discontinuity :

A function f defined on an interval I ⊆ R is said to have removable discontinuity at x₀ ∈ I if there is a function h :

I -> R such that h(x)  =

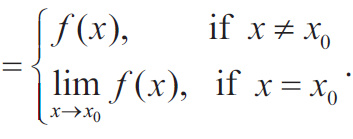
Finding Removable Discontinuity At the given point - Examples

Question 1 :

Which of the following functions f has a removable discontinuity at x = x₀? If the discontinuity is removable, find a function g that agrees with f for x ≠ x₀ and is continuous on R.

(i)  f(x)  =  (x² - 2x - 8)/(x + 2), x₀  =  -2 

Solution :

In order to check if the given function is continuous at the point x₀  =  -2, let us apply -2 

f(x)  =  ((-2)² - 2(-2) - 8)/(-2 + 2),

  =  (4+4-8)/0

  =  0/0 

The given function is not continuous at x = -2. In order to redefine the function, we have to simplify f(x).

f(x)  =  (x² - 2x - 8)/(x + 2)

  =  (x - 4) (x - 2)/(x - 2)

f(x)  =  (x -  4)

f(-2)  =  -2 - 4

=  -6 

Hence the given function has removable discontinuity at x = 2.

By redefining the function, we get

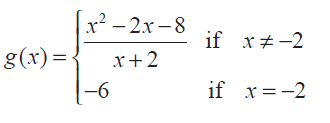
Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.