HYPOTENUSE ACUTE ANGLE THEOREM

Hypotenuse Acute Angle or HA Theorem is the theorem  which can be used to prove the congruence of two right triangles. 

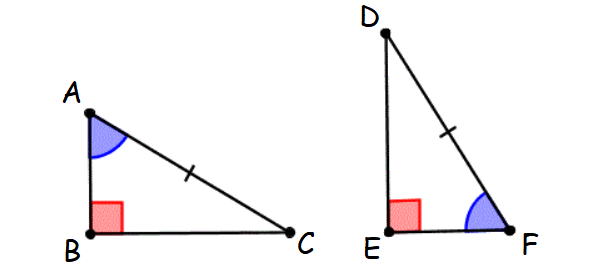
Explanation :

If the hypotenuse and an acute angle of a right triangle are congruent to the hypotenuse and an acute angle of another right triangle, then the two triangles are congruent.

This principle is known as Hypotenuse-Acute Angle theorem. 

Examples

Example 1 :

Check whether two triangles PQR and ABC are congruent.

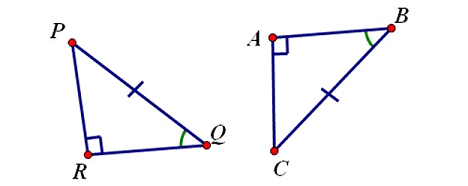
Solution :

(i) PQ  =  BC (Hypotenuse)

(ii) ∠Q  =  ∠B (Acute angle)

Hence, the two triangles PQR and ABC are congruent by Hypotenuse-Acute (HA) Angle theorem.

Example 2 :

Check whether two triangles OPQ and IJK are congruent.

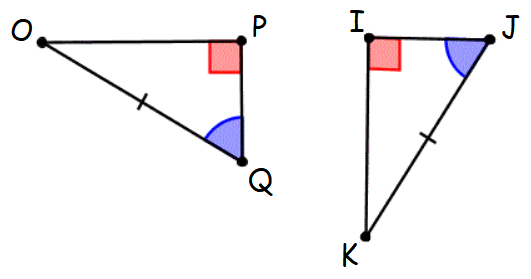
Solution :

(i) Triangle OPQ and triangle IJK are right triangles. Because they both have a right angle. 

(ii) OQ  =  JK (Hypotenuse)

(iii) ∠Q  =  ∠J (Given)

Hence, the two triangles OPQ and IJK are congruent by Hypotenuse-Acute (HA) Angle theorem. 

Other Triangle Congruence Postulates and Theorems

1. Side-Side-Side (SSS) Congruence Postulate

If three sides of one triangle is congruent to three sides of another triangle, then the two triangles are congruent.

2. Side-Angle-Side (SAS) Congruence Postulate

If two sides and the included angle of one triangle are equal to two sides and the included angle of another triangle, then the two triangles are congruent.

3. Angle-Side-Angle (ASA) Congruence Postulate

If two angles and the included side of one triangle are equal to two angles and the included side of another triangle, then the two triangles are congruent.

4. Angle-Angle-Side (AAS) Congruence Postulate

If two angles and non-included side of one triangle are equal to two angles and the corresponding non-included side of another triangle, then the two triangles are congruent.

5. Hypotenuse-Leg (HL) Theorem

If the hypotenuse and one leg of a right triangle are equal to the hypotenuse and one leg of another right triangle, then the two right triangles are congruent.

6. Leg-Acute (LA) Angle Theorem

If a leg and an acute angle of one right triangle are congruent to the corresponding parts of another right triangle, then the two right triangles are congruent.

7. Leg-Leg (LL) Theorem

If the legs of one right triangle are congruent to the legs of another right triangle, then the two right triangles are congruent.

Apart from the problems given above, if you need more problems on triangle congruence postulates,

Please click here

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.