IDENTIFYING FUNCTIONS WORKSHEET WITH ANSWERS

Problem 1 :

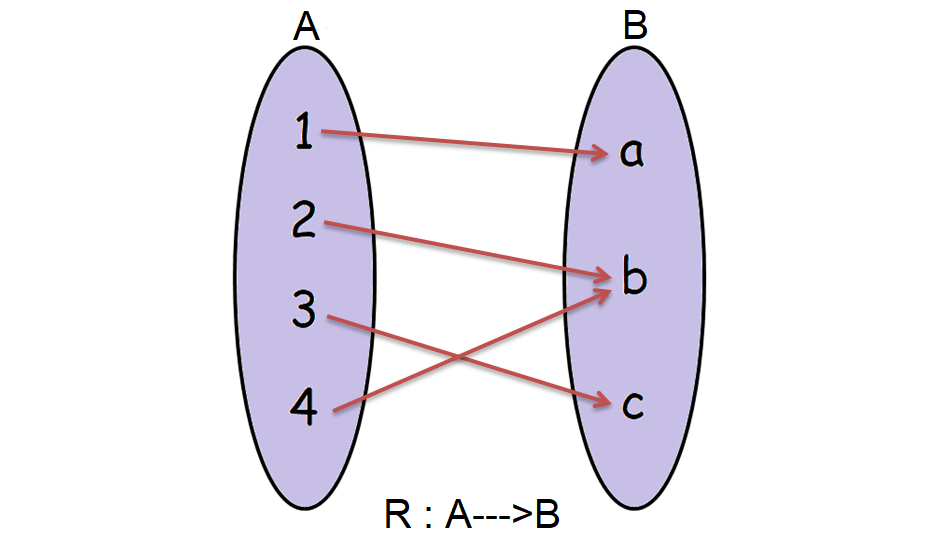
Let A = {1, 2, 3, 4} and B = {a, b, c}. 

Consider the relation R given below which maps the elements from A to B. 

R = {(1, a), (2, b), (3, c), (4, b)}

Determine whether the relationship R is a function.

Problem 2 :

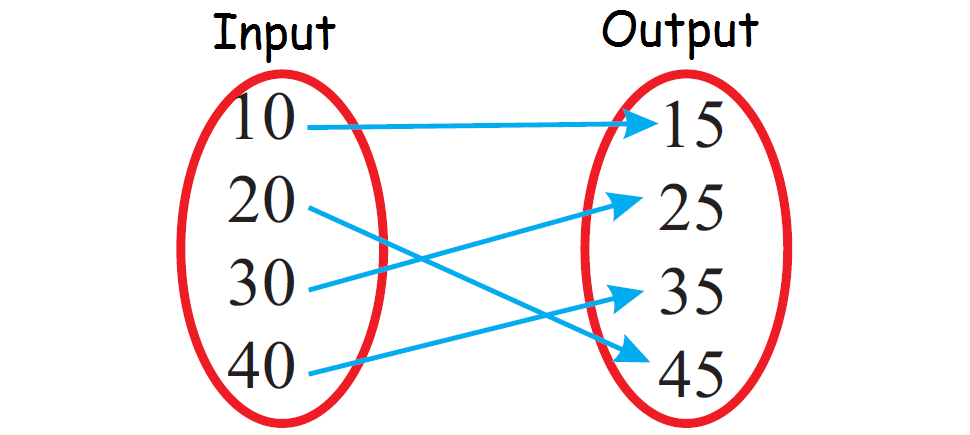
Determine whether the relationship given in the mapping diagram is a function.

Problem 3 :

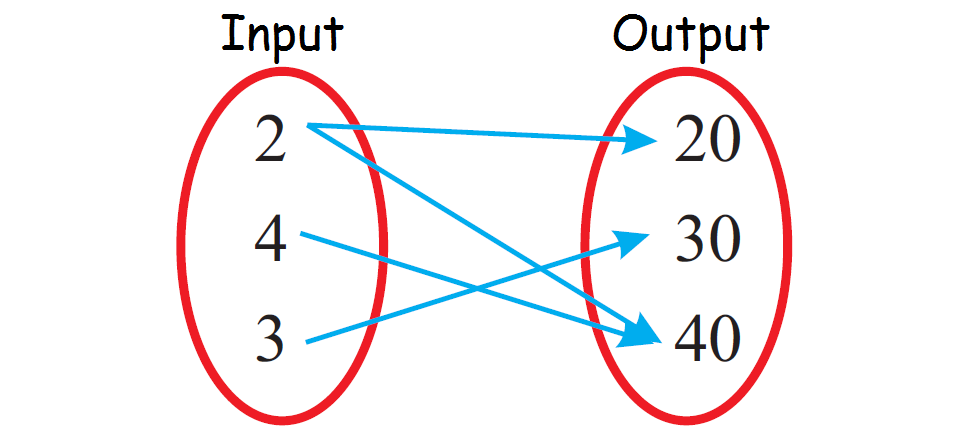
Determine whether the relationship given in the mapping diagram is a function.

Problem 4 :

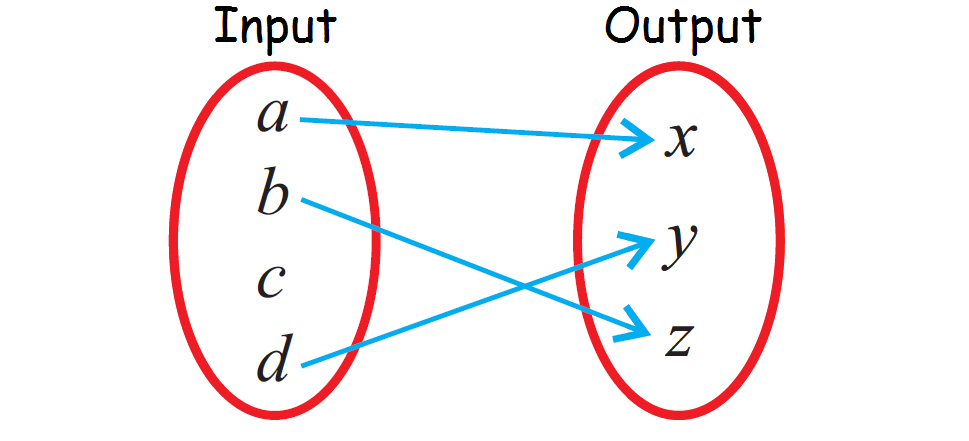
Determine whether the relationship given in the mapping diagram is a function.

Problem 5 :

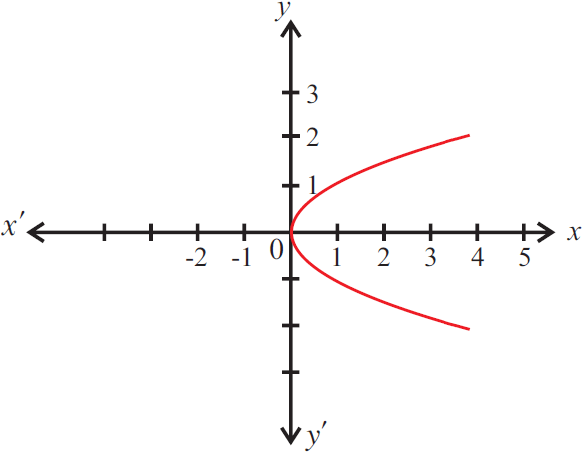
Use the vertical line test to determine which of the following graphs represent a function.

Problem 6 :

Use the vertical line test to determine which of the following graphs represent a function.

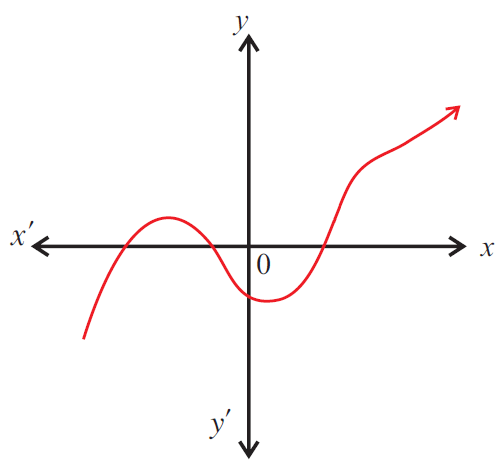
Problem 7 :

Use the vertical line test to determine which of the following graphs represent a function.

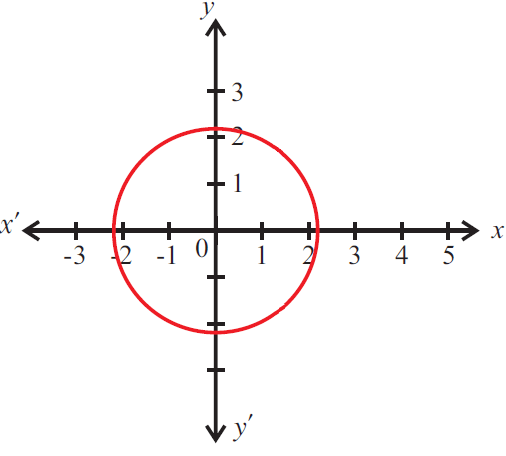
Problem 8 :

Determine whether the relationship given in the table is a function.

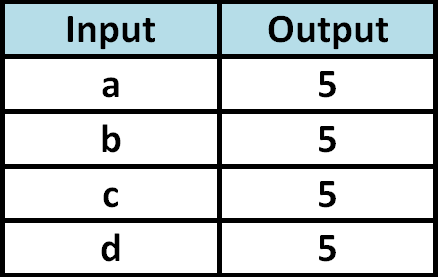
Answers

1. Answer :

In the above relation R, 

Domain (R)  =  A

And also, every element of A has only one image in B. 

So, the relation R is a function. 

It has been illustrated in the picture shown below. 

2. Answer :

Because each input value is paired with only one output value, the relationship given in the above mapping diagram is a function.

3. Answer :

Because 2 is paired with more than one output value (both 20 and 40), the relationship given in the above mapping diagram is not a function.

4. Answer :

Because the input value 'c' is not paired with any output value, the relationship given in the above mapping diagram is not a function.

5. Answer :

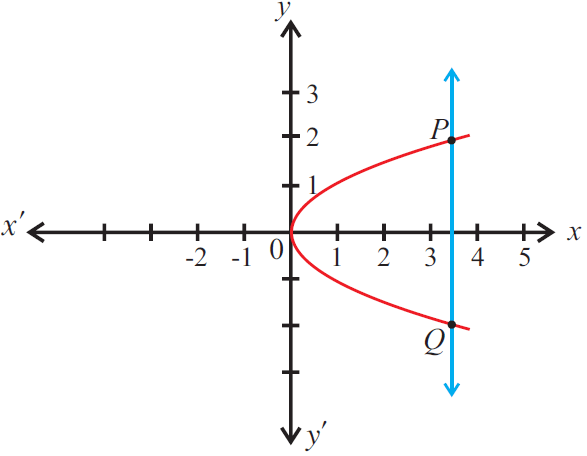
The given graph does not represent a function as a vertical line cuts the graph at two points P and Q.

6. Answer :

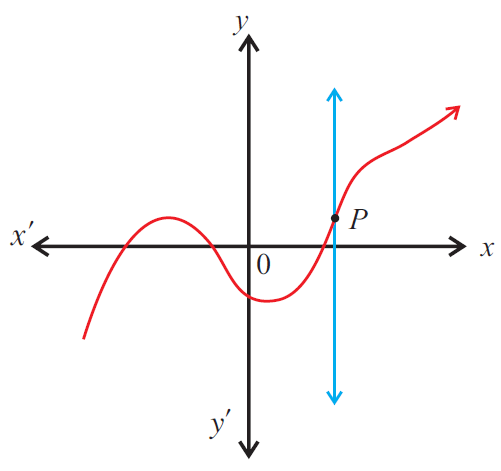
The given graph represents a function as any vertical line will intersect the graph at most one point P.

7. Answer :

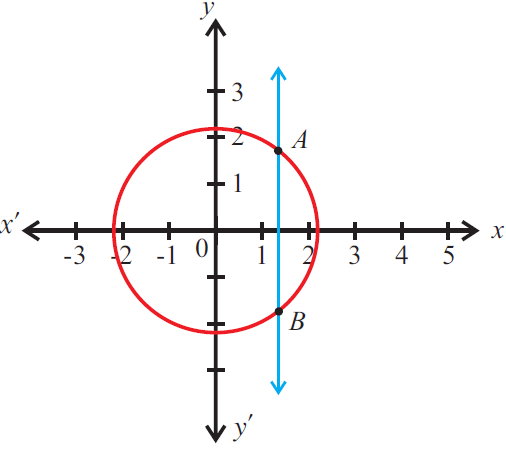
The given graph does not represent a function as a vertical line cuts the graph at two points A and B.

8. Answer :

Because each input value is paired with only one output value, the relationship given in the above table is a function.

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.