IDENTITY FUNCTION

Let A be a non-empty set. A function

f : A ---> A is called an identity-function of A if f(a) = a for all 'a' belonging to A.

That is, an identity function maps each element of A into itself.

For example, let A be the set of real numbers (R). The function f : R ----> R be defined by f (x) = x for all x belonging to  R is the identity-function on R.

The figure given below represents the graph of the identity function on R.

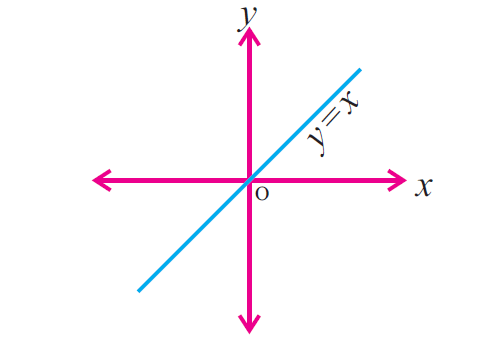
Related Topics

One to one or Injective function

Onto or Surjective function

One to one and Onto or Bijective function

Into function

Constant Function

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.