INCREASING AND DECREASING FUNCTIONS WORKSHEET

Problem 1 : 

The graph shown below gives the weight W of a person at age x. Determine the intervals on which the function W is increasing and on which it is decreasing.

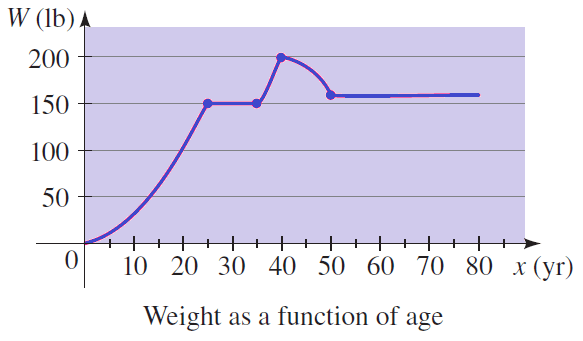
Problem 2 :

(a)  Sketch the graph of the function f(x) = x^2/3.  

(b)  Find the domain and range of the function.

(c)  Find the intervals on which f increases and decreases.

Problem 3 :

The graph of the function shown below has domain [−1, 6].

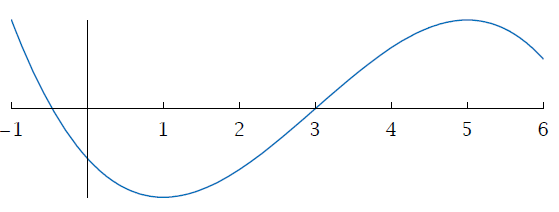
(a) Find the largest interval on which f is increasing.

(b) Find the largest interval on which f is decreasing.

(c) Find the largest interval containing 6 on which f is decreasing.

Problem 4 :

Shown below are the graphs of three functions; each function is graphed on its entire domain.

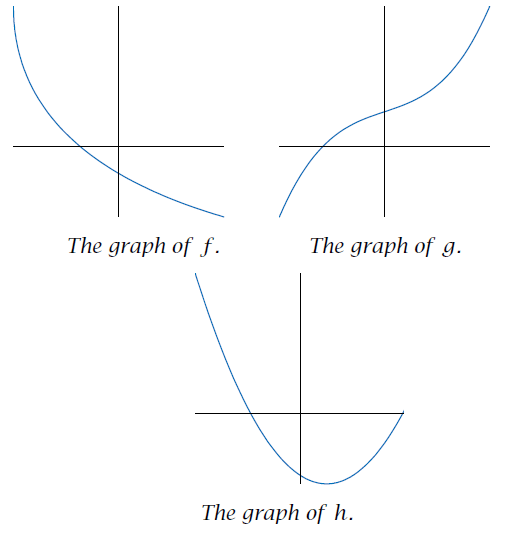
(a) Is f increasing, decreasing, or neither?

(b) Is g increasing, decreasing, or neither?

(c) Is h increasing, decreasing, or neither?

Problem 5 :

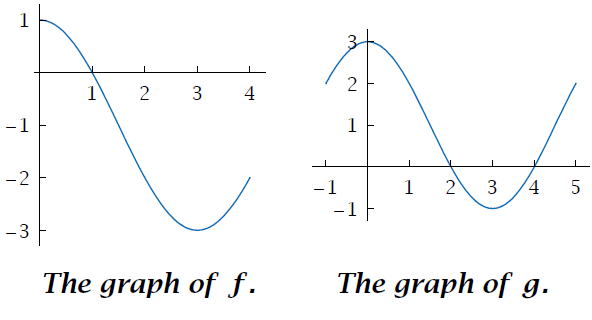
Here f has domain [0, 4] and g has domain [−1, 5].

(i)  What is the largest interval contained in the domain of f on which f is increasing?

(ii)  What is the largest interval contained in the domain of g on which g is increasing?

(a) find the critical numbers of (if any)

(b) find the open interval(s) on which the function is increasing or decreasing

(c) apply the First Derivative Test to identify increasing and decreasing interval

(d) use a graphing utility to confirm your results.

Problem 6 :

f(x) = x² - 4x

Problem 7 :

f(x) = x² - 2x - 8

Problem 8 :

Use the definitions of increasing and decreasing functions to prove that

f(x) = x³

is increasing on (-∞, ∞)

Problem 9 :

Proof Use the definitions of increasing and decreasing functions to prove that 

f(x) = 1/x

is decreasing on (0, ∞).

1. Answer :

The function is increasing on [0, 25] and [35, 40]. It is decreasing on [40, 50]. The function is constant (neither increasing nor decreasing) on [25, 35] and [50, 80]. This means that the person gained weight until age 25, then gained weight again between ages 35 and 40. He lost weight between ages 40 and 50.

2. Answer : 

(a)  We can use a graphing calculator to sketch the graph shown below. 

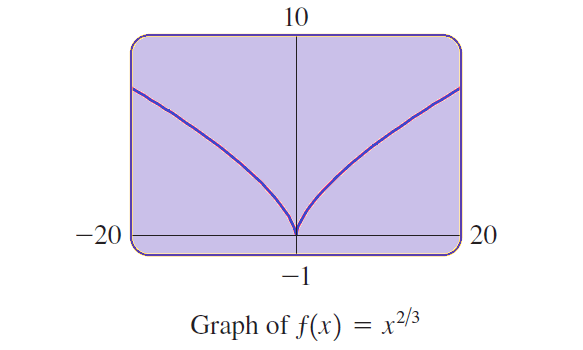
From the graph above, we can observer that

(b)  the domain of f is R and the range is [0, ∞). 

(c)  f is decreasing on (-∞, 0] and increasing on [0, ∞). 

3. Answer :

From the graph above, we can observe,

(a) [1, 5] is the largest interval on which f is increasing.

(b) [−1, 1] is the largest interval on which f is decreasing.

(c) [5, 6] is the largest interval containing 6 on which f is decreasing.

4. Answer :

(a) The graph of f gets lower from left to right on its entire domain. Thus f is decreasing.

(b) The graph of g gets higher from left to right on its entire domain. Thus g is increasing.

(c) The graph of h gets lower from left to right on part of its domain and gets higher from left to right on another part of its domain. Thus h is neither increasing nor decreasing.

5. Answer :

(i) The largest interval on which the function f increasing is [3, 4].

(i) The largest interval on which the function g decreasing is [0, 3].

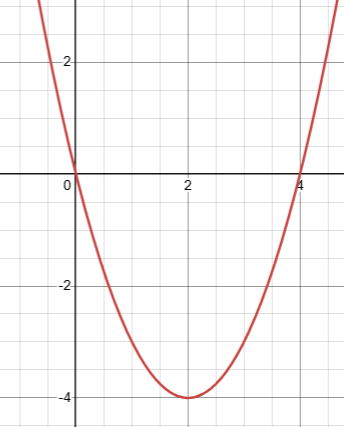
6. Answer :

f(x) = x² - 4x

Finding the first derivative,

f'(x) = 2x - 4

f'(x) = 2(x - 2)

a) Finding critical numbers :

f'(x) = 0

2x - 4 = 0

2x = 4

x = 4/2

x = 2

b) Finding intervals :

(-∞, 2] and [2, ∞)

c)  Increasing in the interval [2, ∞) and decreasing in the interval (-∞, 2].

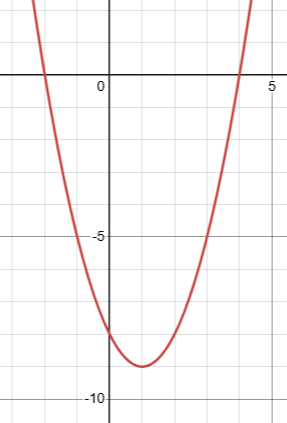
7. Answer :

f(x) = x² - 2x - 8

Finding the first derivative,

f'(x) = 2x - 2

f'(x) = 2(x - 1)

a) Finding critical numbers :

f'(x) = 0

2(x - 1) = 0

x = 1

b) Finding intervals :

(-∞, 1] and [1, ∞)

c)  Increasing in the interval [1, ∞) and decreasing in the interval (-∞, 1].

8. Answer :

Use the definitions of increasing and decreasing functions to prove that

f(x) = x³

is increasing on (-∞, ∞)

Finding the first derivative,

f'(x) = 3x²

In the derivative function, we have x squared term along with positive coefficient. Whatever values, we apply in the place of x, we get only positive value for f'(x).

So, the function is increasing in all real numbers. That is, it is increasing in the interval (-∞, ∞).

9. Answer :

Proof Use the definitions of increasing and decreasing functions to prove that 

f(x) = 1/x

is decreasing on (0, ∞).

Given that, f(x) = 1/x = x^-1

f'(x) = -1x^-2

= -1/x²

Even though we have x squared term in the derivative function, since we have negative coefficient, it must be decreasing function and 0 should not included. 

For all positive and negative values of x, we get only negative numbers as results. So, it is decreasing in the interval (0, ∞).

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.