INDIRECT PROOF AND INEQUALITIES IN TWO TRIANGLES

An indirect proof is a proof in which we prove that a statement is true by first assuming that its opposite is true. If this assumption leads to an impossibility, then we have proved that the original statement is true.

Guidelines for Writing an Indirect Proof

1. Identify the statement that you want to prove.

2. Begin by assuming the statement is false; assume its opposite is true.

3. Obtain statements that logically follow from your assumption.

4. If you obtain a contradiction, then the original statement must be true.

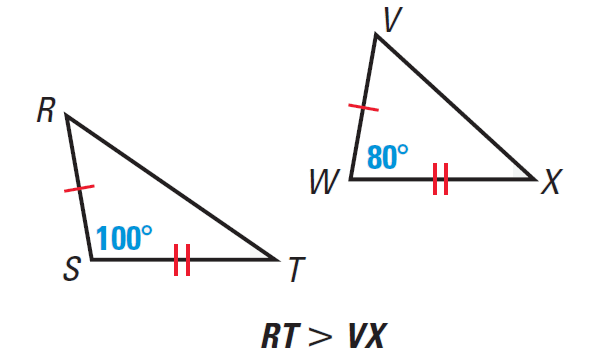
Hinge Theorem

If two sides of one triangle are congruent to two sides of another triangle, and the included angle of the first is larger than the included angle of the second, then the third side of the first is longer than the third side of the second.

It has been illustrated in the diagram given below.

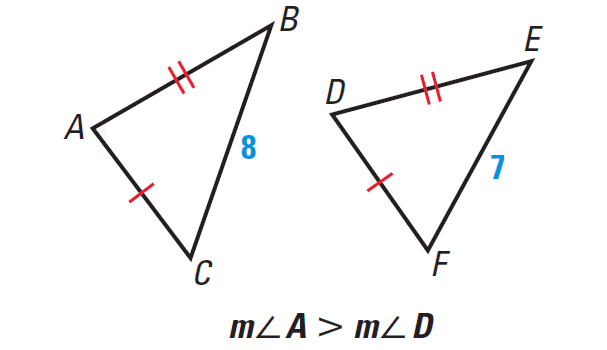
Converse of the Hinge Theorem

If two sides of one triangle are congruent to two sides of another triangle, and the third side of the first is longer than the third side of the second, then the included angle of the first is larger than the included angle of the second.

It has been illustrated in the diagram given below.

Example 1 :

Use an indirect proof to prove that a triangle cannot have more than one obtuse angle.

Solution :

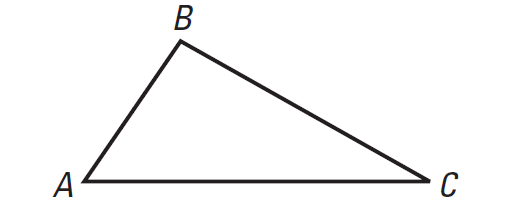
Given : Triangle ABC

To Prove : Triangle ABC does not have more than one obtuse angle.

Begin by assuming that triangle ABC does have more than one obtuse angle.

We know, however, that the sum of the measures of all three angles is 180°.

So, we can plug 180° - m∠C for m∠A + m∠B in

m∠A + m∠B > 180°

The last statement is not possible.

Because angle measures in any triangle cannot be negative.

So, we can conclude that the original assumption must be false. That is, triangle ABC cannot have more than one obtuse angle.

Example 2 :

Use an indirect proof to prove the Converse of the Hinge Theorem.

Solution :

Converse of the Hinge Theorem :

If two sides of one triangle are congruent to two sides of another triangle, and the third side of the first is longer than the third side of the second, then the included angle of the first is larger than the included angle of the second.

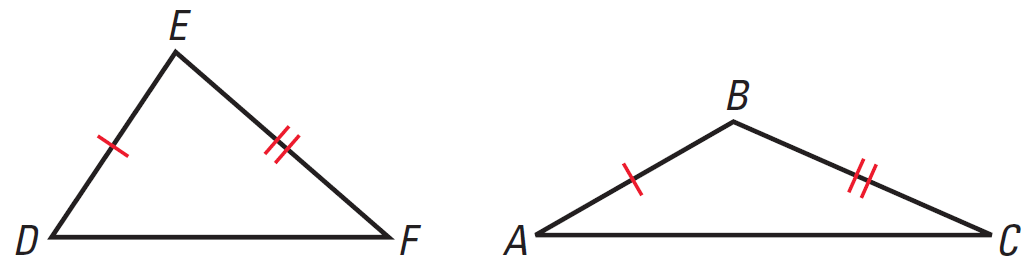
Given :

AB ≅ DE

BC ≅ EF

AC > DF

To Prove :

m∠B > m∠E

Begin by assuming that m∠B  is not greater than m∠E.

Then, it follows that either m∠B = m∠E or m∠B < m∠E.

Case 1 :

If m∠B = m∠E, then m∠B ≅ m∠E.

So, ΔABC  ≅  ΔDEF by the SAS Congruence Postulate and AC = DF.

Case 2 :

If m∠B  <  m∠E, then AC  <  DF by the Hinge theorem.

Both conclusions contradict the given information that

AC > DF

So the original assumption that m∠B is not greater than m∠E cannot be correct.

Therefore,

m∠B > m∠E

Example 3 :

In triangles ABC and DEF, we have

AB ≅ DE

BC ≅ EF

AC = 12 inches 

m∠B = 36°

m∠E = 80°

Which of the following is a possible length for DF?

8 inches, 10 inches, 12 inches, 23 inches

Solution :

From the given information, let us draw the two triangles ABC and DEF.

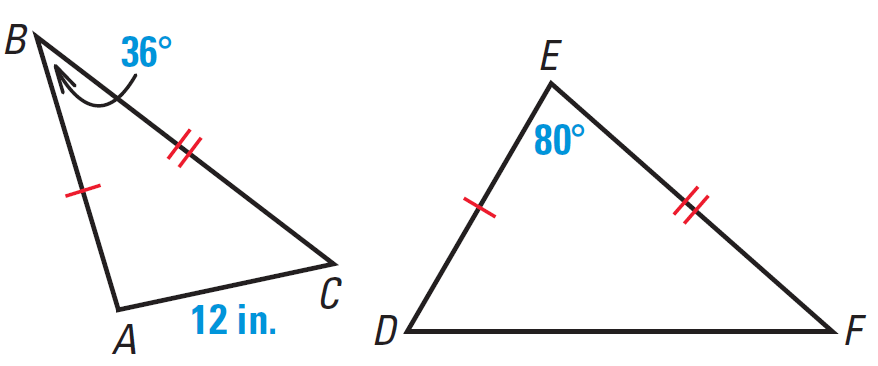
Because the included angle in triangle DEF is larger than the included angle in triangle ABC, the third side DF must be longer than AC.

So, of the four choices, the only possible length for DF is 23 inches. The diagram of the two triangles ABC and DEF above shows that this is possible.

Example 4 :

In triangles RST and XYZ, we have

RT ≅ XZ

ST ≅ YZ

RS = 3.7 centimeters

XY = 4.5 centimeters

m∠Z = 75°

Which of the following is a possible measure for m∠T?

60°, 75°, 90°, 105°

Solution :

Because the third side in triangle RST is shorter than the third side in triangle XYZ, the included angle m∠T must be smaller than m∠Z.

So, of the four choices, the only possible measure for m∠T is 60°.

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.