INEQUALITIES IN ONE TRIANGLE

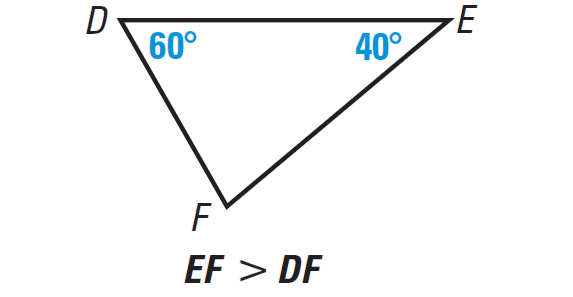
Theorem 1 :

If one side of a triangle is longer than another side, then the angle opposite the longer side is larger than the angle opposite the shorter side.

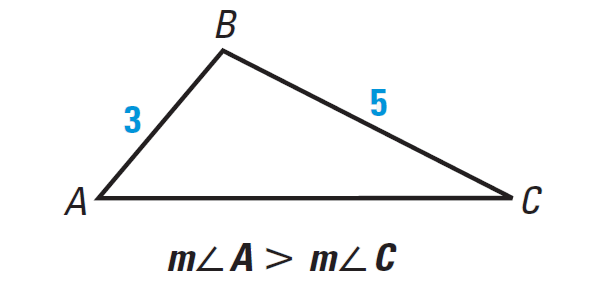
Theorem 2 :

If one angle of a triangle is larger than another angle, then the side opposite the larger angle is longer than the side opposite the smaller angle.

Exterior Angle Inequality

The measure of an exterior angle of a triangle is greater than the measure of either of the two nonadjacent interior angles.

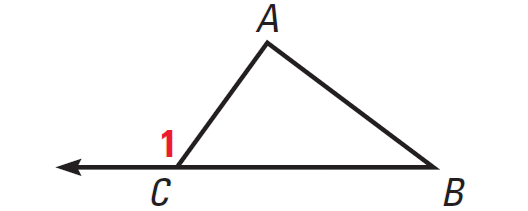
In the triangle above, according to theorem 3, we have

m∠1 > m∠A

m∠1 > m∠B

Triangle Inequality

The sum of the lengths of any two sides of a triangle is greater than the length of the third side.

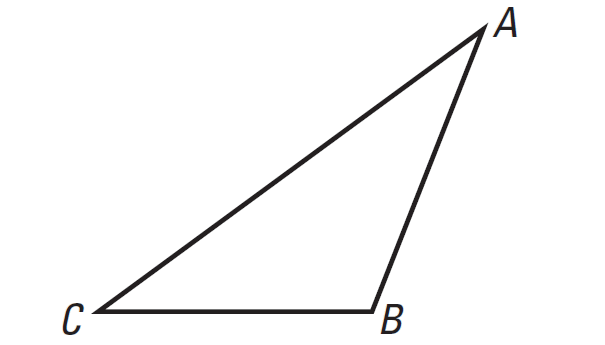
In the triangle ABC above, according to theorem 4, we have

AB + BC > AC

AC + BC > AB

AB + AC > BC

Solved Examples

Example 1 :

Write the sides of the triangle shown below in order from least to greatest.

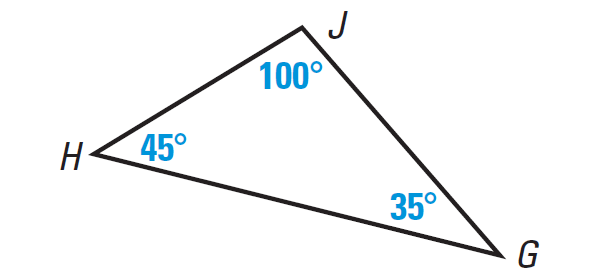
Solution :

In the triangle GHJ above, we have

m∠G < m∠H < m∠J

So, the smallest angle is m∠G and the largest angle m∠J.

In any triangle, the smallest angle is always across from the shortest side and the largest angle is always across from the longest side.

Hence, the order of sides of the triangle from least to greatest is

JH < JG < GH

Example 2 :

Write the angles of the triangle shown below in order from smallest to largest.

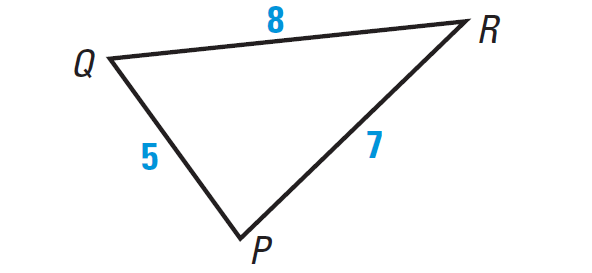
Solution :

In the triangle PQR above, we have

PQ < PR < QR

So, the shortest side is PQ and the longest side is QR.

In any triangle, the smallest angle is always across from the shortest side and the largest angle is always across from the longest side.

Hence, the order of angles of the triangle from smallest to largest is

m∠R < m∠Q < m∠P

Example 3 :

In the triangle shown below AB ≅ AC and BC > AB. What can we conclude about the angles in triangle ABC ?

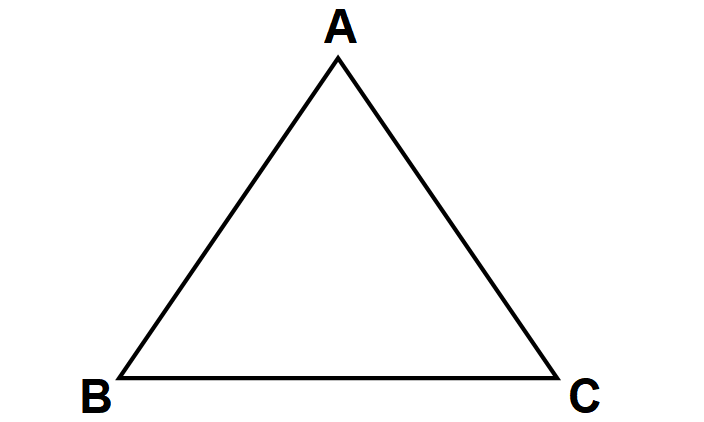
Solution :

Because AB ≅ AC, triangle ABC is isosceles.

So, we have

m∠B ≅ m∠C

Therefore, m∠B = m∠C.

Because BC > AB, m∠A > m∠C by Theorem 1.

By substitution, m∠A > m∠B.

In addition, you can conclude that m∠A > 60°. m∠B < 60° and m∠C < 60°.

Example 4 :

Construct a triangle with the given group of side lengths, if possible.

2 cm, 2 cm, 5 cm

Solution :

We can not construct a triangle with the given side lengths.

Because, sum of the lengths of any two sides of a triangle must be greater than the third side by Theorem 4.

In the given side lengths, we have

2 + 2 < 5

(Does not satisfy the theorem)

The diagram given below illustrates that a triangle can not be constructed with the given side lengths.

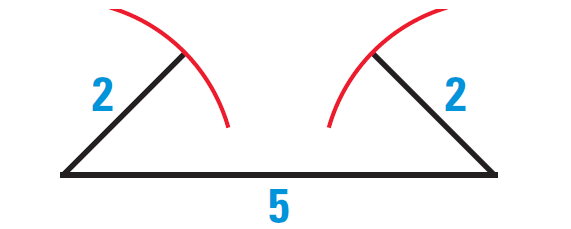
Example 5 :

Construct a triangle with the given group of side lengths, if possible.

3 cm, 2 cm, 5 cm

Solution :

We can not construct a triangle with the given side lengths.

Because, sum of the lengths of any two sides of a triangle must be greater than the third side by Theorem 4.

In the given side lengths, we have

3 + 2  =  5

(Does not satisfy the theorem)

The diagram given below illustrates that a triangle can not be constructed with the given side lengths.

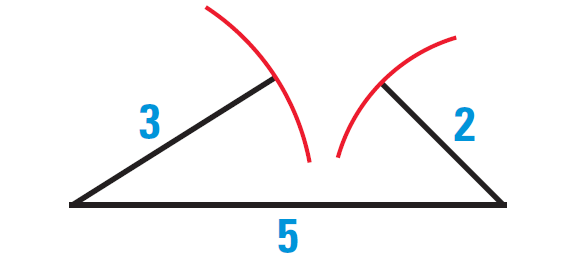
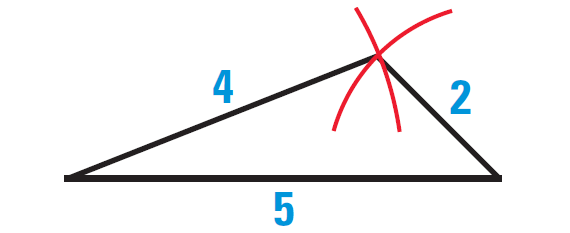
Example 6 :

Construct a triangle with the given group of side lengths, if possible.

4 cm, 2 cm, 5 cm

Solution :

In the given side lengths, we have

4 + 2 > 5

4 + 5 > 2

2 + 5 > 4

In the given side lengths, it is clear that the sum of any two sides is greater than the third side.

Because the given side lengths satisfy Theorem 4, we can construct a triangle with the given side lengths.

The diagram given below illustrates that a triangle can be constructed with the given side lengths.

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.