INJECTIVE SURJECTIVE AND BIJECTIVE FUNCTIONS

In this section, you will learn the following three types of functions. 

(i) One to one or Injective function

(ii) Onto or Surjective function

(iii) One to one and onto or Bijective function

One to one or Injective Function

Let f : A ----> B be a function.

The function f is called an one to one, if it takes different elements of A into different elements of B.

That is, we say f is one to one

In other words f is one-one, if no element in B is associated with more than one element in A.

A one-one function is also called an Injective function.

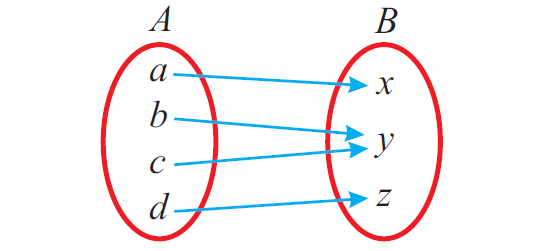
The figure given below represents a one-one function.

Onto or Surjective Function

Let f : A ----> B be a function.

The function f is called an onto function, if every element in B has a pre-image in A.

That is, in B all the elements will be involved in mapping. 

An onto function is also called a surjective function.

The figure given below represents a onto function.

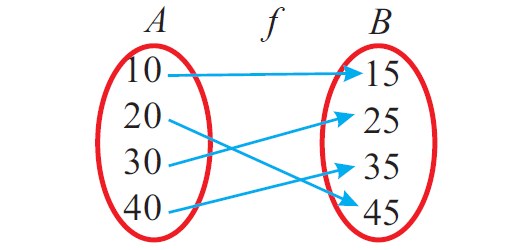
One to One and Onto or Bijective Function

Let f : A ----> B be a function.

The function f is called as one to one and onto or a bijective function, if f is both a one to one and an onto function

More clearly,

f maps distinct elements of A into distinct images in B and every element in B is an image of some element in A.

The figure shown below represents a one to one and onto or bijective function.

Solved Problems

Problem 1 : 

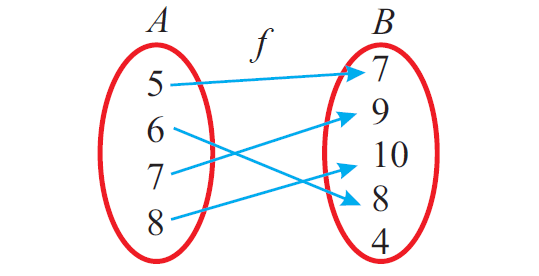
Let f : A ----> B. A, B and f are defined as 

A  =  {1, 2, 3}

B  =  {5, 6, 7, 8}

f  =  {(1, 5), (2, 8), (3, 6)}

Verify whether f is a function. if so, what type of function is f ?

Solution :

Write the elements of f (ordered pairs) using arrow diagram as shown below

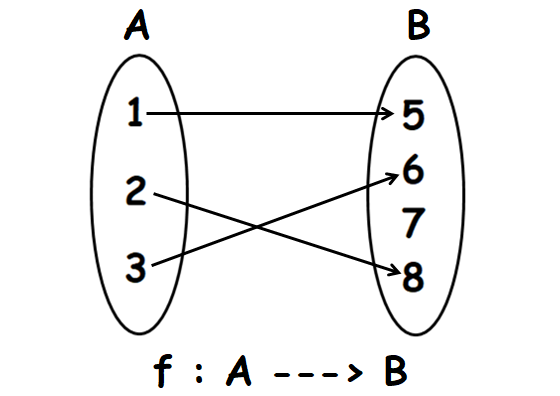
In the above arrow diagram, all the elements of A have images in B and every element of A has a unique image.

That is, no element of A has more than one image.

So, f is a function. 

Every element of A has a different image in B.

That is, no two or more elements of A have the same image in B.

Therefore, f is one to one or injective function.

Problem 2 : 

Let f : X ----> Y. X, Y and f are defined as 

X  =  {a, b, c, d}

Y  =  {d, e, f}

f  =  {(a, e), (b, f), (c, e), (d, d)}

Verify whether f is a function. if so, what type of function is f ?

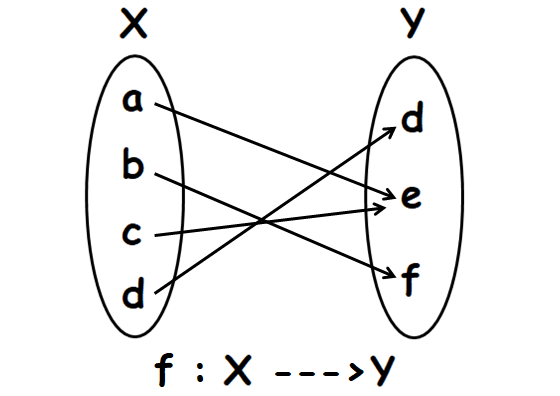
In the above arrow diagram, all the elements of X have images in Y and every element of X has a unique image.

That is, no element of X has more than one image.

So, f is a function. 

Every element of Y has a pre-image in X. 

Therefore, f is onto or surjective function. 

Problem 3 : 

Let f : A ----> B. A, B and f are defined as 

A  =  {1, 2, 3, 4}

B  =  {5, 6, 7, 8}

f  =  {(1, 8), (2, 6), (3, 5), (4, 7)}

Verify whether f is a function. if so, what type of function is f ?

Solution :

Write the elements of f (ordered pairs) using arrow diagram as shown below. 

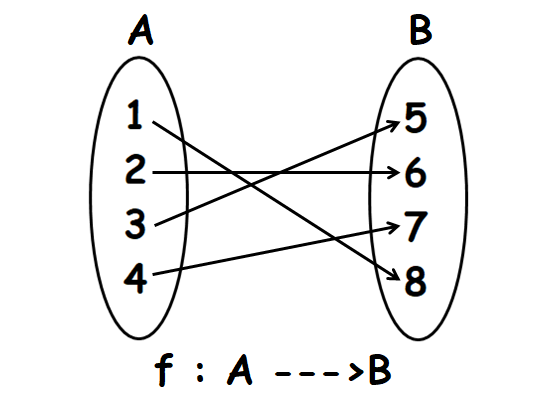
In the above arrow diagram, all the elements of A have images in B and every element of A has a unique image.

That is, no element of A has more than one image.

So, f is a function. 

Every element of B has a pre-image in A. So f is onto function. 

Every element of A has a different image in B.

That is, no two or more elements of A have the same image in B.

Therefore, f is one to one and onto or bijective function.

Related Topics

Into function

Constant Function

Identity function

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.