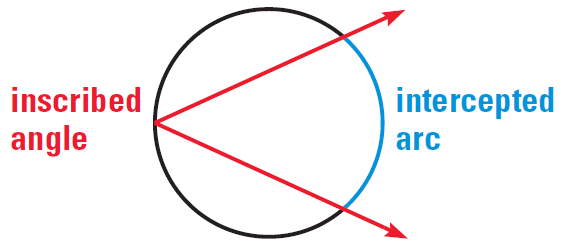
INSCRIBED ANGLES IN A CIRCLE

An inscribed angle is an angle whose vertex is on a circle and whose sides contain chords of the circle.  The arc that lies in the interior of an inscribed angle and has endpoints on the angle is called the intercepted arc of the angle.

Theorem (Measure of an Inscribed Angle)

If an angle is inscribed in a circle, then its measure is half the measure of its intercepted arc.

It has been illustrated below. 

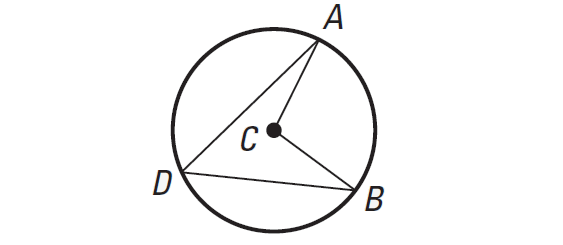
In the diagram shown above, we have

m∠ ADB  =  1/2 ⋅ m∠arc AB

Theorem on Two Inscribed Angles  

If two inscribed angles of a circle intercept the same arc, then the angles are congruent.

It has been illustrated below. 

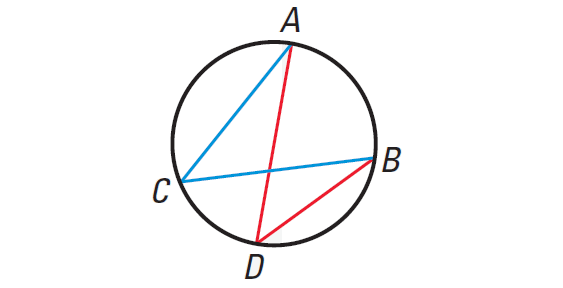
In the diagram shown above, we have 

m∠C  ≅  m∠D  

Finding Measures of Arcs and Inscribed Angles 

Example 1 :

Find the measure of the blue arc. 

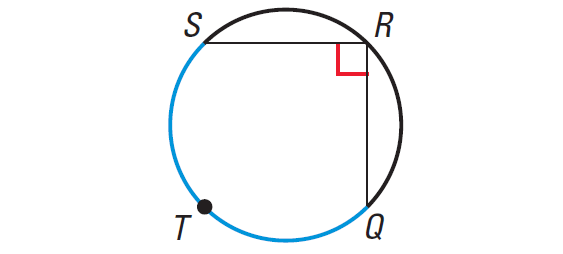
Solution :

m∠arc QTS  =  2 ⋅ m∠QRS  =  2 ⋅ 90°  =  180°

Example 2 :

Find the measure of the blue arc. 

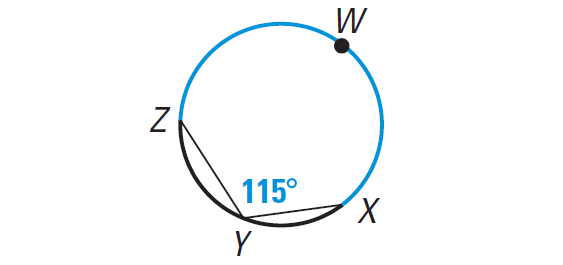
Solution :

m∠arc ZWX  =  2 ⋅ m∠ZYX  =  2 ⋅ 115°  =  230°

Example 3 :

Find the measure of the blue angle. 

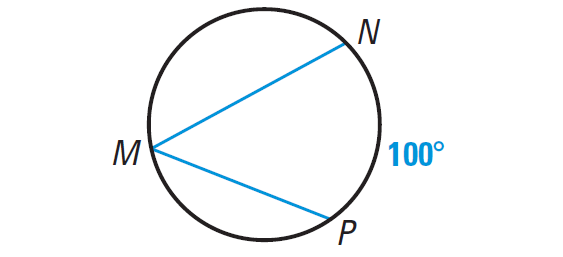
Solution :

m∠NMP  =  1/2 ⋅ m∠arc NP  =  1/2 ⋅ 100°  =  50°

Comparing Measures of Inscribed Angles

Example 4 :

Find m∠ACB, m∠ADB, and m∠AEB in the diagram shown below. 

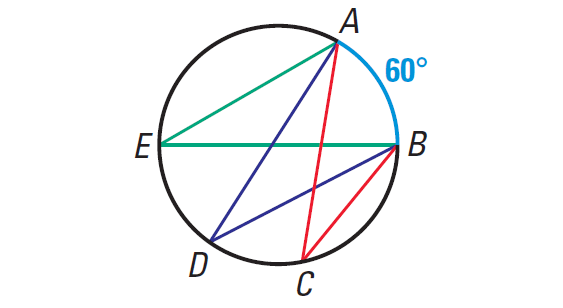
Solution :

In the diagram shown above, the inscribed angles m∠ACB, m∠ADB, and m∠AEB intercept the same arc AB. 

So, the measure of each angle is half the measure of arc AB. 

That is,

m∠arc AB  =  60°

So the measure of each angle is 30°.

That is, 

m∠ACB  =  m∠ADB  =  m∠AEB  =  60°

Finding the Measure of an Angle

Example 5 :

In the diagram shown below, it is given that m∠E = 75°.  What is m∠F ?

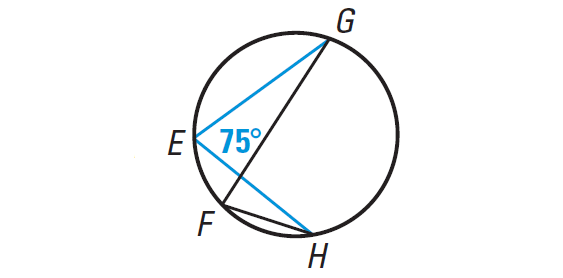
Solution :

m∠E and m∠F both intercept arc GH, so ∠E ≅ ∠F.

So, we have

m∠F  =  m∠E  =  75°

Using the Measure of an Inscribed Angle

Example 6 :

When we go to the movies, we may want to be close to the movie screen, but we don’t want to have to move our eyes too much to see the edges of the picture. 

In the diagram shown below, if E and G are the ends of the screen  and we are at F, m∠EFG is called our viewing angle.

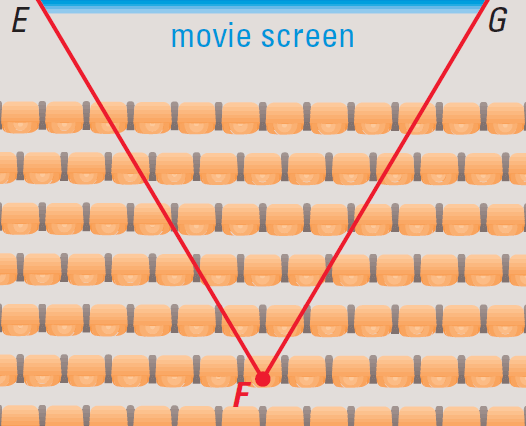
We decide that the middle of the sixth row has the best viewing angle.  If someone is sitting there, where else can we sit to have the same viewing angle ?

Solution :

Draw the circle that is determined by the endpoints of the screen and the sixth row center seat. Any other location on the circle will have the same viewing angle as shown below.

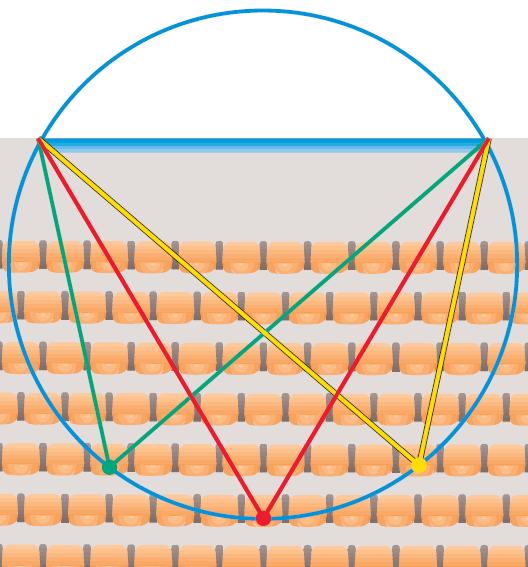
Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.