INSCRIBED QUADRILATERALS WORKSHEET

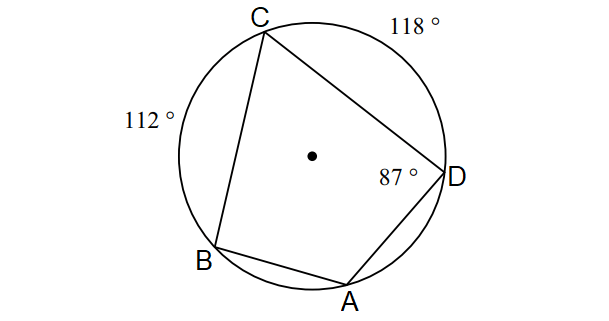
Problem 1 : 

In the diagram shown below, find the following measures :

m∠A, m∠B and m∠C

Problem 2 : 

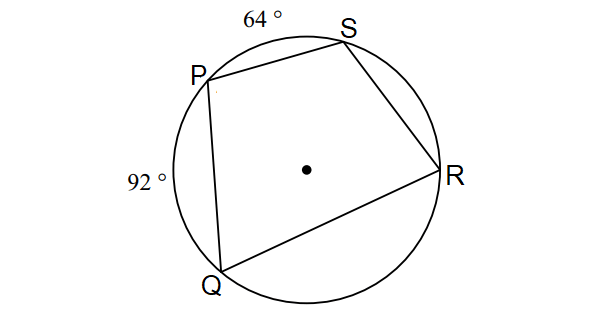
In the diagram shown below, find the following measures :

m∠P and m∠R

Problem 3 :

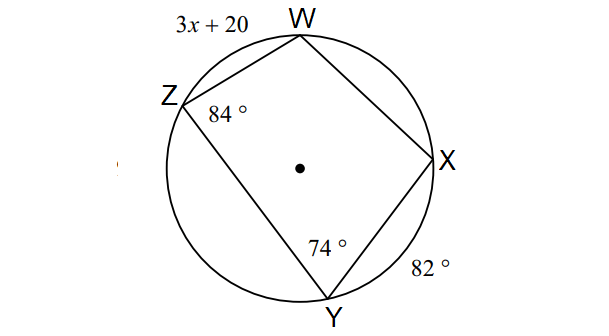
In the diagram shown below, find the value of x.

Problem 4 :

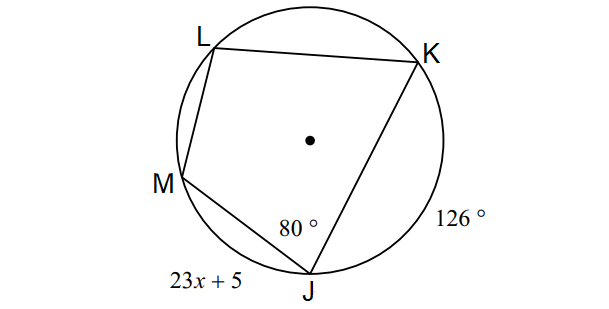
In the diagram shown below, find the value of x.

Problem 5 :

In the diagram shown below, find the value of x.

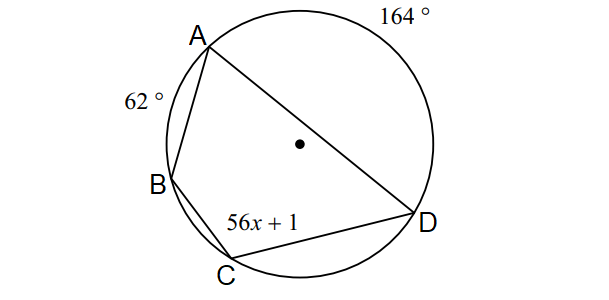
Problem 6 :

In the diagram shown below, find the value of x.

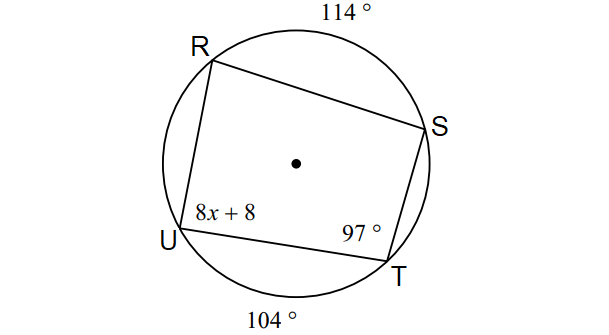
Problem 7 :

In the diagram shown below, find the values of x and y.

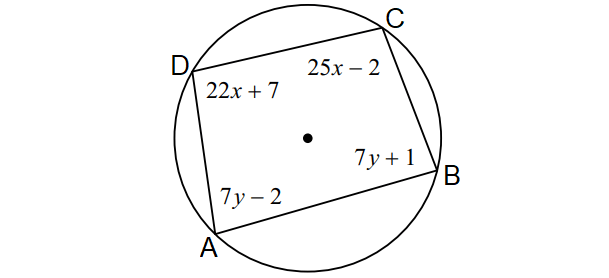
Answers

1. Answer :

In the above diagram, quadrilateral ABCD is inscribed in a circle. Then, its opposite angles are supplementary.  

m∠A + m∠C = 180° ----(1)

m∠B + m∠D = 180° ----(2)

In (2), substitute m∠D = 87°.

m∠B + 87° = 180°

Subtract 87° from both sides.

m∠B = 93°

In the circle above,

m∠arc BC + m∠arc CD + m∠arc BAD = 360°

112° + 118° + m∠arc BAD = 360°

230° + m∠arc BAD = 360°

Subtract 230° from each side. 

m∠arc BAD = 130°

By Inscribed Angle Theorem, 

m∠C = 1/2 ⋅ m∠arc BAD

m∠C = 1/2 ⋅ 130°

m∠C = 65°

In (1), substitute m∠C = 65°.

m∠A + 65° = 180°

Subtract 65° from both sides.

m∠A = 115°

2. Answer :

In the circle above,

m∠arc PQ + m∠arc PS + m∠arc QRS = 360°

92° + 64° + m∠arc QRS = 360°

156° + m∠arc QRS = 360°

Subtract 156° from both sides. 

m∠arc QRS = 204°

By Inscribed Angle Theorem, 

m∠P = 1/2 ⋅ m∠arc QRS

m∠P = 1/2 ⋅ 204°

m∠P = 102°

In the above diagram, quadrilateral PQRS is inscribed in a circle. Then, its opposite angles are supplementary.  

m∠P + m∠R = 180°

Substitute m∠P = 102°.

102° + m∠R = 180°

Subtract 102° from both sides.

m∠R = 78°

3. Answer :

In the diagram above, by Inscribed Angle Theorem,

m∠arc WXY = 2m∠Z

Substitute m∠Z = 84°.

m∠arc WXY = 2(84°)

m∠arc WXY = 168°

m∠arc WX + m∠arc XY = 168°

Substitute m∠arc XY = 82°.

m∠arc WX + 82° = 168°

Subtract 82° from both sides.

m∠arc WX = 86°

Again, by Inscribed Angle Theorem,

m∠arc ZWX = 2m∠Y

m∠arc ZW + m∠arc WX = 2m∠Y

Substitute.

3x + 20 + 86 = 2(74)

3x + 106 = 148

Subtract 106 from both sides.

3x = 42

Divide both sides by 3.

x = 14

4. Answer :

In the diagram above, by Inscribed Angle Theorem,

m∠arc MLK = 2m∠J

Substitute m∠J = 80°.

m∠arc MLK = 2(80°)

m∠arc MLK = 160°

In the circle above,

m∠arc MJ + m∠arc JK + m∠arc MLK = 360°

Substitute.

23x + 5 + 126 + 160 = 360

23x + 291 = 360

Subtract 291 from both sides.

23x = 69

Divide both sides by 23.

x = 3

5. Answer :

In the diagram above, by Inscribed Angle Theorem,

m∠C = 1/2 ⋅ m∠arc BAD

m∠C = 1/2 ⋅ (m∠arc BA + m∠arc AD)

Substitute.

56x + 1 = 1/2 ⋅ (62 + 164)

56x + 1 = 1/2 ⋅ (226)

56x + 1 = 113

Subtract 1 from both sides.

56x = 112

Divide both sides by 56.

x = 2

6. Answer :

In the diagram above, by Inscribed Angle Theorem,

m∠arc URS = 2∠T

m∠arc UR + m∠arc RS = 2∠T

Substitute.

m∠arc UR + 114° = 2(97°)

m∠arc UR + 114° = 194°

Subtract 114° from both sides.

m∠arc UR = 80°

Again, by Inscribed Angle Theorem,

m∠S = 1/2 ⋅ m∠arc RUT

m∠S = 1/2 ⋅ (m∠arc UR + m∠arc UT)

Substitute.

m∠S = 1/2 ⋅ (80° + 104°)

m∠S = 1/2 ⋅ 184°

m∠S = 92°

In the above diagram, quadrilateral PQRS is inscribed in a circle. Then, its opposite angles are supplementary.  

m∠U + m∠S = 180°

Substitute.

8x + 8 + 92 = 180

8x + 100 = 180

Subtract 100 from both sides.

8x = 80

Divide both sides by 8.

x = 10

7. Answer :

In the above diagram, quadrilateral ABCD is inscribed in a circle. Then, its opposite angles are supplementary.

(1) - (2) :

3x = 12

Divide both sides by 3.

x = 4

Substitute x = 4 in (1).

25(4) + 7y = 184

100 + 7y = 184

7y = 84

y = 12

Therefore,

x = 4 and y = 12

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.