INTEGRATE QUADRATIC FUNCTION IN THE DENOMINATOR

We have to express ax²+bx+c as sum or difference of two square terms to get the integrand in one of the standard forms.

Example 1 :

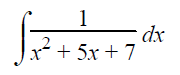
Solution :

We should represent the quadratic equation which is in the denominator in the form of sum or difference of squares.

Using completing the square method, we get

=  x² + 2 ⋅x ⋅ (5/2)  + (5/2)² - (5/2)²+7

=  (x+(5/2))²+7-25/4

=  (x+(5/2))²+3/4

=  (x+(5/2))²+(√3/2)²

This exactly matches the formula,

∫1/(x²+a²) dx  =  1/a tan^-1(x/a) + c

Here a  =  √3/2 and x  = x+(5/2)

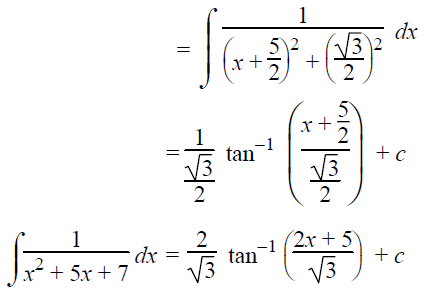
Example 2 :

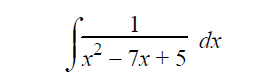
Solution :

Using completing the square method, we get

=  x² - 2 ⋅x ⋅ (7/2)  + (7/2)² - (7/2)²+5

=  x² - 2 ⋅x ⋅ (7/2)  + (7/2)² - (49/4)+5

=  (x-(7/2))²+5-49/4

=  (x-(7/2))²-29/4

=  (x-(7/2))²-(√29/2)²

This exactly matches the formula,

∫1/(x²-a²) dx  =  (1/2a) [log (x-a)/(x+a)] + c

Here a  =  √29/2 and x  = x-(7/2)

Integrating Quadratic Function in the Denominator with Square Root

Example 3 :

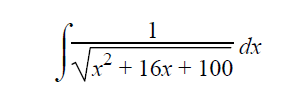
Solution :

Using completing the square method, we get 

=  x² + 2⋅x⋅8 + 8²-8²+100

=  (x+8)² -64+100

=  (x+8)²+36

=  (x+8)²+6²

This exactly matches the formula,

∫1/√(a²+x²) dx  =  log[x+√(a²+x²)] + c

Here a  =  6 and x  = x+8

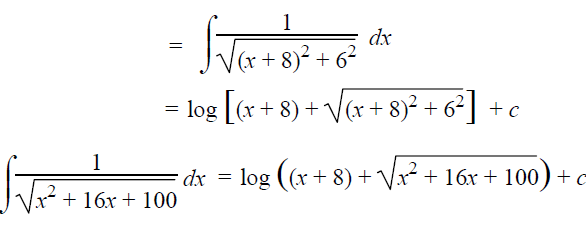
Example 4 :

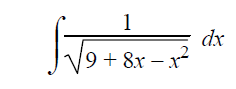
Solution :

Using completing the square method, we get 

9+8x-x²  =  -(x²-8x-9)

=  -(x² - 2⋅x⋅4 + 4²-4²-9)

=  -[(x-4)²-16-9]

=  -[(x-4)²-25]

=  5²-(x-4)²

This exactly matches the formula,

∫1/√(a²-a²) dx  =  sin^-1(x/a) + C

Here a  =  5 and x  =  x-4

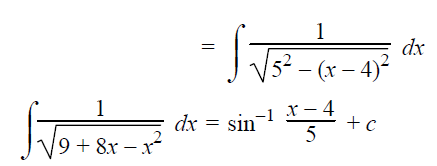
Integration of Rational Functions by Partial Fractions

Example 5 :

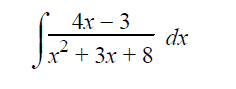
Using partial fraction, we are decomposing

∫(4x-3)/(x²+3x+8) dx 

Numerator  =  A (Derivative of denominator) + B  --(1)

4x-3  =  A d(x²+3x+8)/dx + B

4x-3  =  A (2x+3) + B

Equating the coefficients of x, we get

4  =  2A

A  =  2

Equating constants, we get

-3  =  3A + B

By applying the value of A, we get

-3  =  6 + B

B  =  -9

Numerator  =  A (Derivative of denominator) + B

Dividing (1) by (x²+3x+8), we get

∫(4x-3)/(x²+3x+8) dx

=  ∫2 (2x+3)/(x²+3x+8) dx - ∫9/(x²+3x+8) dx

=  2∫[(2x+3)/(x²+3x+8)]dx - 9∫[1/(x²+3x+8)] dx

By integrating 2∫[(2x+3)/(x²+3x+8)]dx :

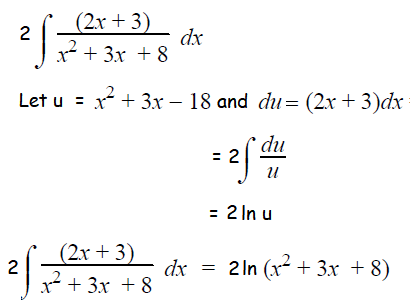
By integrating 9∫1/(x²+3x+8)dx :

Using completing the square method, we get

=  x² + 2⋅x⋅(3/2) + (3/2)²-(3/2)²+8

=  (x+(3/2))² + 8 - 9/4

=  (x+(3/2))² + 23/4

=  (x+(3/2))² + √(23/2)²

The second part exactly matches with the formula

∫1/(x²+a²) dx  =  1/a tan^-1(x/a) + c

Here x  =  x+(3/2) and a  =  √(23/2)

Using the above formula, we get

=  1/√(23/2) tan^-1 (2x+3)/√23

=  (2/√23) tan^-1 (2x+3)/√23

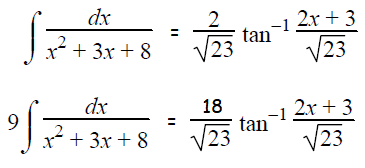
By combing the above results, we get

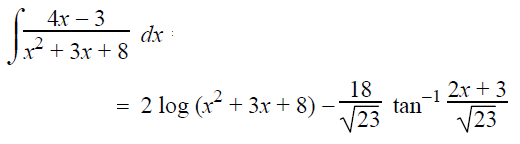
Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.