INTEGRATION USING BERNOULLIS FORMULA
The evaluation of an indefinite integral of the form
∫ u(x) v(x)dx
becomes very simple, when u is a polynomial function of x and v(x) can be easily integrated successively.
It is accomplished by a formula called Bernoulli’s formula. This formula is actually an extension of the formula of integration by parts. To derive the formula, we use the following notation:
∫ udv = uv-u'v1+u''v2 - +u'''v3 +...........
The above result is called the Bernoulli’s formula for integration of product of two functions.
Note :
Since u is a polynomial function of x , the successive derivative u(m)will be zero for some positive integer m and so all further derivatives will be zero only.
Hence the right-hand-side of the above formula contains a finite number of terms only.
Evaluate the following.
Problem 1 :
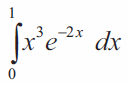
Solution :
= e-2 (1-3/2 - 6/4 - 6/16) + 3/8
= e-2 (1-3/2 - 3/2 - 3/8) + 3/8
= e-2 (1-6/2 - 3/8) + 3/8
= e-2 (8-24-3)/8 + 3/8
= -19e-2/8 + 3/8
Problem 2 :
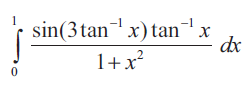
Solution :
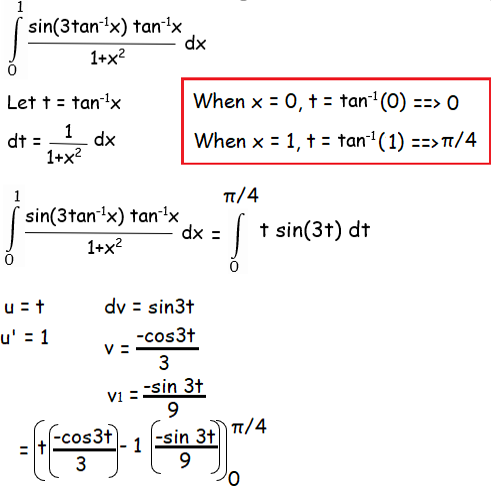
= π/4 [(-cos 3π/4)/3] + sin(3π/4)/9 - 0 - 0
= π/4 [(1/3√2)] + 1/9√2
= π/12√2 + 1/9√2
= (1/√2)[π/12 + 1/9]
Problem 3 :
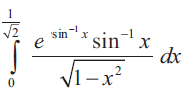
Solution :
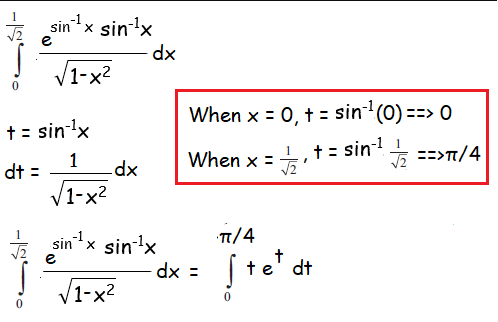
Using Bernoulli's theorem,
u = t, dv = et dt
u' = 1, v = et dt and v1 = et
= [tet - 1et] limits 0 to π/4
= [π/4eπ/4 - 1eπ/4 + 1]
= eπ/4(π/4 - 1) + 1
Problem 4 :
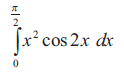
Solution :
Let u = x2 and dv = cos 2x
u' = 2x, u'' = 2
v = sin 2x/2, v1 = -cos2x/4, v2 = -sin2x/8
= [x2(sin 2x/2) - 2x (-cos2x/4) + 2(-sin2x/8)] 0 to π/2
By applying the limit, we get
= -π/4
Kindly mail your feedback to v4formath@gmail.com
We always appreciate your feedback.
©All rights reserved. onlinemath4all.com
Recent Articles
-
Digital SAT Math Problems and Solutions (Part - 62)
Nov 05, 24 11:16 AM
Digital SAT Math Problems and Solutions (Part - 62) -
SAT Math Resources (Videos, Concepts, Worksheets and More)
Nov 05, 24 11:15 AM
SAT Math Resources (Videos, Concepts, Worksheets and More) -
Worksheet on Proving Trigonometric Identities
Nov 02, 24 11:58 PM
Worksheet on Proving Trigonometric Identities
