INTERCEPT FORM EQUATION OF A LINE
We will find the equation of a line whose intercepts are 'a' and 'b' on the coordinate axes respectively.
Let PQ be a line meeting X axis at A and Y axis at B.
Let OA = a, OB = b. Then the coordinates of A and B are (a, 0) and (0, b) respectively.
Therefore, the equation of the line joining A and B is
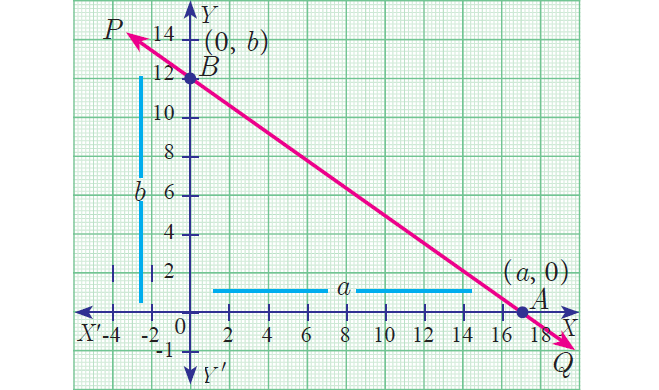
Using two-point form, equation of line joining the two points A and B is
(y - 0)/(b - 0) = (x - a)/(0 - a)
y/b = -(x - a)/a
y/b = (-x + a)/a
y/b = -x/a + 1
Hence, Intercept-Form equation of a line is
x/a + y/b = 1
Example 1 :
If the x-intercept and y-intercept of a straight line are 2 and -4 respectively, find the general equation of the straight line.
Solution :
Given : x- intercept is 2 and y-intercept is -4.
Equation of a straight line in intercept form :
x/a + y/b = 1
Substitute a = 2 and b = -4.
x/2 + y/(-4) = 1
x/2 - y/4 = 1
Least common multiple of the denominators 2 and 4 is 4.
Multiply each side by 4 to get rid of the fractions.
2x - y = 4
Subtract 4 from each side.
2x - y - 4 = 0
Example 2 :
Find the intercepts made by the line 4x + 9y - 36 = 0 on the coordinate axes.
Solution :
Write the equation in intercept form.
4x + 9y - 36 = 0
Add 36 to each side.
4x + 9y = 36
Divide each side by 36.
(4x + 9y)/36 = 36/36
4x/36 + 9y/36 = 1
x/9 + y/4 = 1
x-intercept = 9
y-intercept = 4
Example 3 :
Find the equation of a line in standard form which passes through (7, 5) and makes intercepts on the axes equal in magnitude but opposite in sign.
Solution :
Let 'a' the x-intercept of the line.
Then y-intercept is '-a'.
Equation of line in intercept form :
x/a + y/b = 1
Substitute b = -a.
x/a + y/(-a) = 1
x/a - y/a = 1
(x - y)/a = 1
x - y = a ----(1)
The line is passing through the point (7, 5).
So, substitute x = 7 and y = 5.
7 - 5 = a
2 = a
Substitute a = 2 in (1).
x - y = 2
Example 4 :
A line makes positive intercepts on coordinate axes whose sum is 7 and it passes through (-3, 8) . Find the equation of line in standard form.
Solution :
Let 'a' and 'b' be the intercepts.
a + b = 7
b = 7 - a
Intercept-form equation of a line :
x/a + y/b = 1
Substitute b = 7 - a.
x/a + y/(7 - a) = 1
–3(7 – a) + 8a = a(7 – a)
-21 + 3a + 8a = 7a - a2
a2 + 4a - 21 = 0
(a - 3)(a + 7) = 0
a = 3 or a = -7
Since a is positive,
a = 3
b = 7 – a = 7 – 3 = 4
Equation of line :
x/3 + y/4 = 1
Least common multiple of the denominators 3 and 4 is 12.
Multiply each side by 12 to get rid of the fractions.
4x + 3y = 12
Kindly mail your feedback to v4formath@gmail.com
We always appreciate your feedback.
©All rights reserved. onlinemath4all.com
Recent Articles
-
Derivative of Absolute Value of x Using Limit Definition
Apr 23, 25 11:11 AM
Derivative of Absolute Value of x Using Limit Definition -
Digital SAT Math Problems and Solutions (Part - 149)
Apr 23, 25 02:33 AM
Digital SAT Math Problems and Solutions (Part - 149) -
Digital SAT Math Problems and Solutions (Part - 148)
Apr 22, 25 08:20 AM
Digital SAT Math Problems and Solutions (Part - 148)