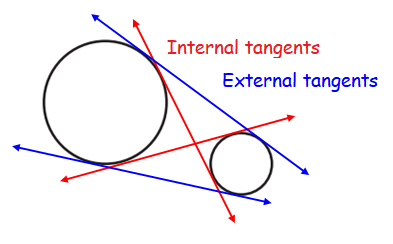
INTERNAL AND EXTERNAL TANGENTS OF A CIRCLE
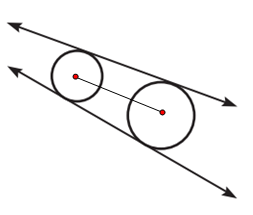
Lines are internal tangents, if they
intersect the segment joining the centers of two circles
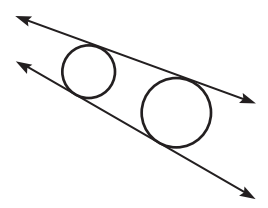
External tangents are lines that do not
cross the segment joining the centers of the circles.
Tell whether the common tangent(s) are internal or external.
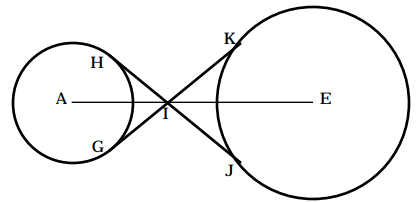
Question 1 :
Solution :
When we draw segments from the center of the circle, it does not intersect the tangents. So, they are external tangents.
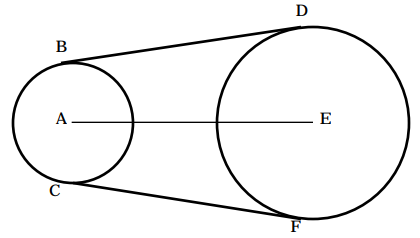
Question 2 :
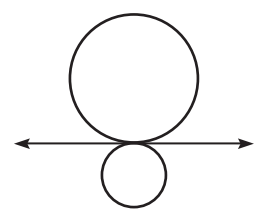
Solution :
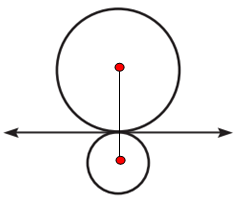
When we draw segments from the center of the circle, it intersects the tangents. So, it is internal tangent.
Question 3 :
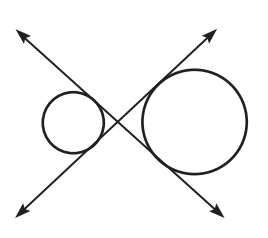
Solution :
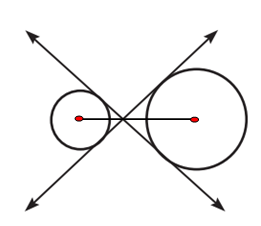
When we draw segments from the center of the circle, it intersects the tangents. So, they are internal tangents.
Copy the diagram. Tell how many common tangents the circles have. Then sketch the tangents.
Question 1 :
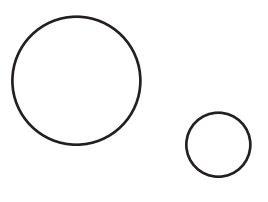
Solution :
We can draw 2 internal tangents and 2 external tangents.
Question 2 :
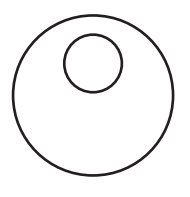
Solution :
We cannot draw any common tangents for the given circles.
Question 3 :
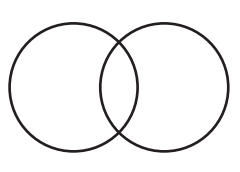
Solution :
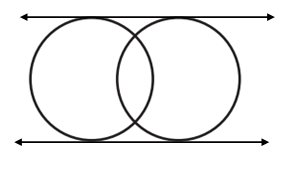
We can two common tangents for the circles given above and they are external tangents.
Are these lines internally or externally tangent? Connect the centers and apply the definitions. Are the circles tangent internally or externally?
Question 4 :
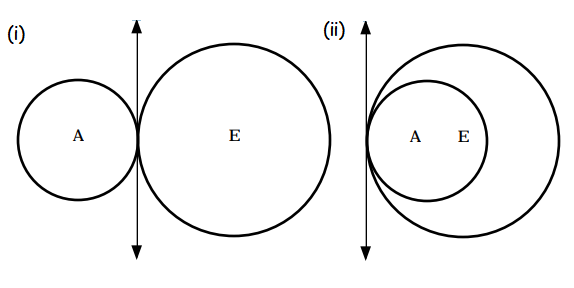
Solution :
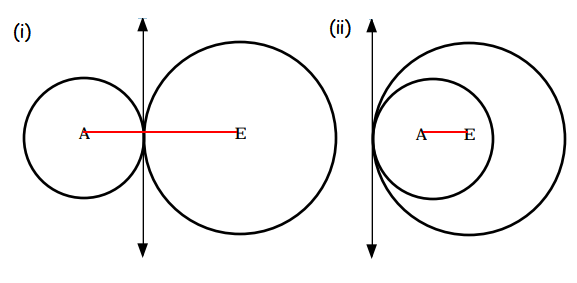
(i) The line segment joining the centers is intersecting the the common tangent. So, it is internal tangent.
(ii) The line segment joining the centers is not intersecting the the common tangent. So, it is external tangent.
Question 5 :
In the diagram P and Q are tangent circles. RS is a common tangent. Find RS.
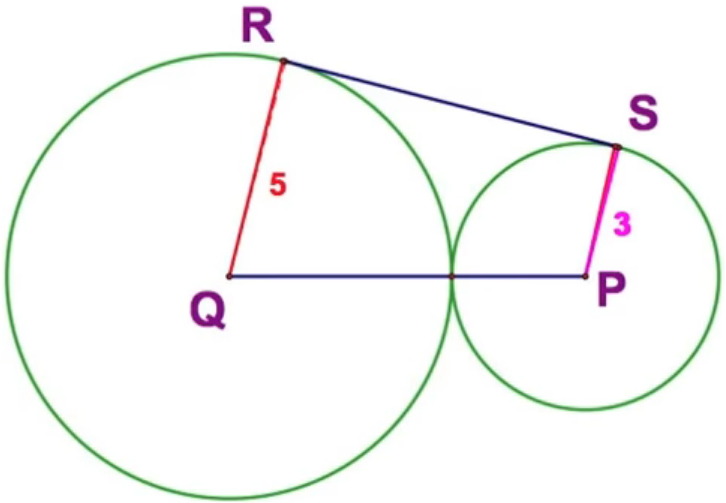
Solution :
RS is a external tangent.
Tangents are perpendicular to the radius at the point of tangency.
<QRS = <PSR = 90 degree
We can connect a point on RQ from P. So, it will create the rectangle PSRT.
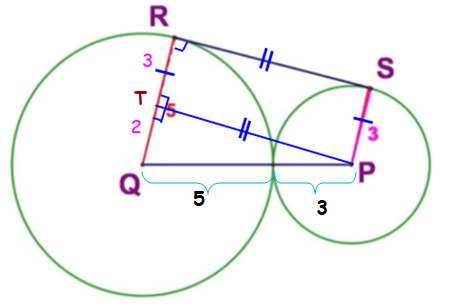
In triangle TPQ,
QP2 = TQ2 + TP2
82 = 22 + TP2
64-4 = TP2
TP = √60
TP = 2√15
RS = 2√15
Question 6 :
If two circles are internally tangent, what is the total number of common tangents that can be drawn to the circle ?
a) 1 b) 2 c) 3 d) 0
Solution :
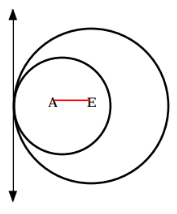
In the picture shown above, we see two circles touches each other internally. So, maximum number of tangents can be drawn is 1.
Question 7 :
JH is tangent to a circle G at J. Find the value of x.
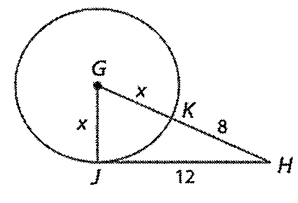
Solution :
By observing the circle above, GK and GJ are radii of the circle.
JH is the tangent and the line drawn from the center of the circle to the point of tangency, then it must be perpendicular.
GH2 = GJ2 + JH2
(x + 8)2 = x2 + 122
x2 + 2x(8) + 82 = x2 + 144
16x + 64 = 144
16x = 144 - 64
16x = 80
x = 80/16
x = 5
So, the radius of the circle is 5 cm.
Question 8 :
AB and AC are tangents to circle O. AB = 4x2 - 42, AC = 17x and OC = 6x + 15. Find OC.
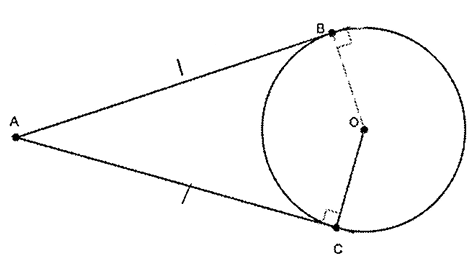
Solution :
Given that, AB = 4x2 - 42, AC = 17x
In general, the length of tangents drawn from the external point of the circle will be equal.
AB = AC
4x2 - 42 = 17x
4x2 - 17x - 42 = 0
4x2 - 24x + 7x - 42 = 0
4x(x - 6) + 7(x - 6) = 0
(4x + 7)(x - 6) = 0
Equating each factor to 0, we get
|
4x + 7 = 0 4x = -7 x = -7/4 |
x - 6 = 0 x = 6 |
To find the length of OC, we have to apply the value of x in the expression OC. Since one of the value is negative, we cannot accept that.
OC = 6(6) + 15
OC = 36 + 15
= 51
So, the radius is 51 cm.
Question 9 :
Two circles have a common external tangent. The radius of one circle is 10 cm. The radius of the other circle is 19 cm. The distance between the centers of the circles is 41 cm. Find the length of the common tangent.
Solution :
By understanding the information, we draw the picture given below.
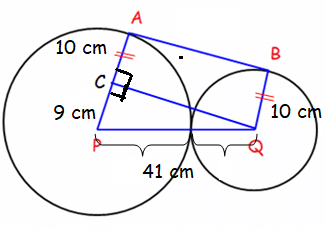
In triangle ACQ,
CQ = x, PC = 9 cm and PQ = 41
It is a right triangle. In every right triangle Pythagorean theorem will exists.
PQ2 = PC2 + CQ2
412 = 92 + x2
x2 = 1681 - 81
x2 = 1600
x = √1600
x = 40
So, the length of CQ is 40 cm.
Question 10 :
AB and AC are tangents of circle with center O and OC = 5x. Find OC.
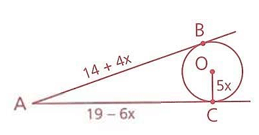
Solution :
Tangents drawn from the external point will have equal length.
AB = AC
14 + 4x = 19 - 6x
4x + 6x = 19 - 14
10x = 5
x = 5/10
x = 1/2
OC = 5x
= 5(1/2)
OC = 5/2 ==> 2.5
Kindly mail your feedback to v4formath@gmail.com
We always appreciate your feedback.
©All rights reserved. onlinemath4all.com
Recent Articles
-
Digital SAT Math Problems and Solutions (Part - 150)
Apr 25, 25 11:46 AM
Digital SAT Math Problems and Solutions (Part - 150) -
AP Calculus AB Problems with Solutions (Part - 19)
Apr 24, 25 11:10 PM
AP Calculus AB Problems with Solutions (Part - 19) -
AP Calculus AB Problems with Solutions (Part - 18)
Apr 24, 25 11:06 PM
AP Calculus AB Problems with Solutions (Part - 18)
