INTRODUCTION TO PERIMETER CIRCUMFERENCE AND AREA
Perimeter :
Perimeter is a path that surrounds a two dimensional shape. The term may be used either for the path or its length it can be thought of as the length of the outline of a shape.
Circumference :
The perimeter of a circle or ellipse is called its circumference. In other words, the distance around the edge of a circle or any curvy shape.
Area :
Area of an object is defined as the space occupied by the object on a flat surface. The area of a shape can be measured by comparing the shape to squares of a fixed size.
Perimeter, Circumference and Area Formulas
Formulas for the perimeter P, area A, circumference C of some common figures are given below.
Square :
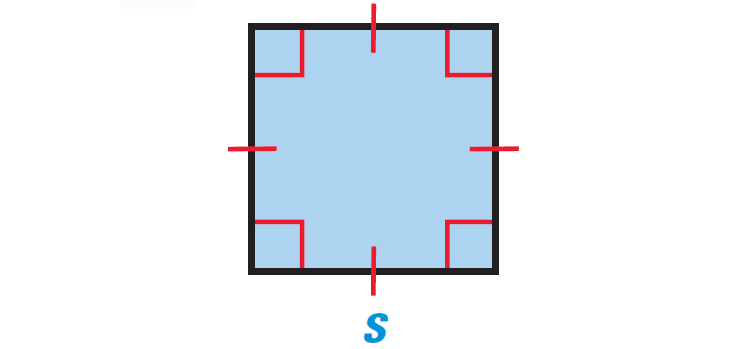
side length = s
Perimeter = 4s
Area = s2
Rectangle :
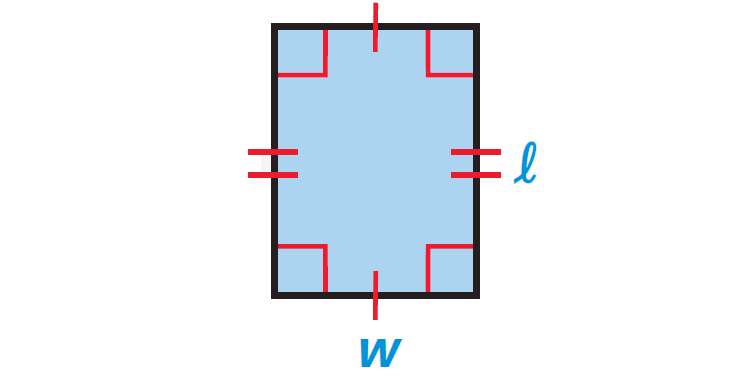
length = l and width = w
Perimeter = 2l + 2w
Area = lw
Triangle :
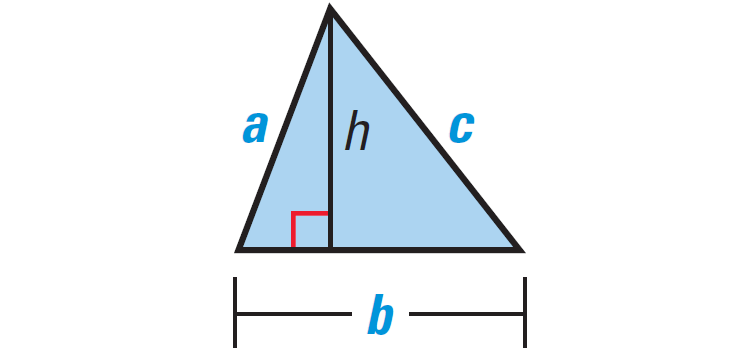
side lengths a, b and c, base = b and height = h
Perimeter = a + b + c
Area = (1/2) ⋅ b ⋅ c
Circle :
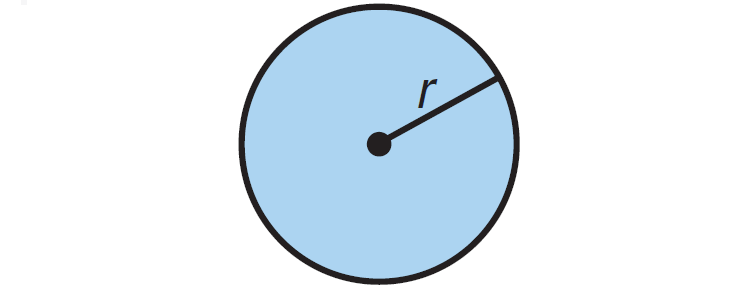
radius = r
Circumference = 2πr
Area = πr2
The measurements of perimeter and circumference use units such as centimeters, meters, kilometers, inches, feet, yards, and miles. The measurements of area use units such as square centimeters (cm2), square meters(m2), and so on.
Example 1 :
Find the perimeter and area of a rectangle of length 12 inches and width 5 inches.
Solution :
Draw a rectangle and label the length and width.
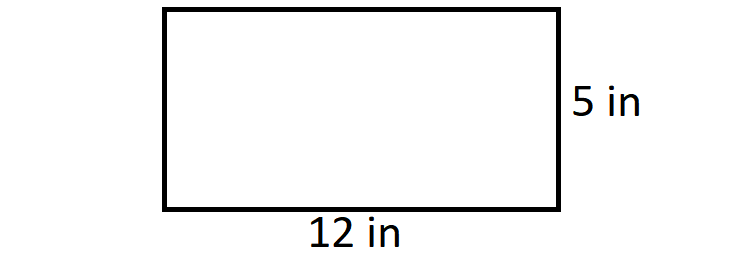
|
Perimeter = 2l + 2w = 2(12) + 2(5) = 24 + 10 = 34 |
Area = lw = 12 ⋅ 5 = 60 |
So, the perimeter is 34 inches and the area is 60 square inches.
Example 2 :
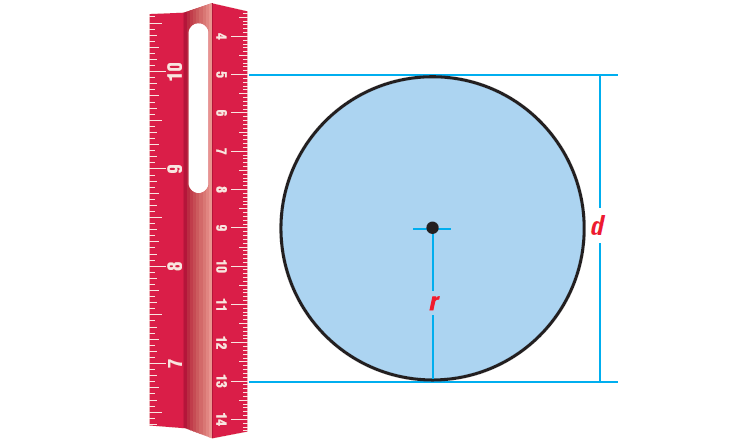
Find the diameter, radius, circumference and area of the circle shown below. use 3.14 as an approximation for π.
Solution :
From the diagram shown above, we can see that the diameter of the circle is
d = 13 - 5 = 8 cm
The radius is one half the diameter. So, the radius is
r = d/2 = 8/2 = 4 cm
Using the formula for circumference, we have
C = 2πr ≈ 2(3.14)(4)
C ≈ 25.1 cm
Using the formulas for area, we have
A = πr2 ≈ (3.14)(4)2
A ≈ 50.24 square cm.
Example 3 :
Find the area and perimeter of the triangle shown below.
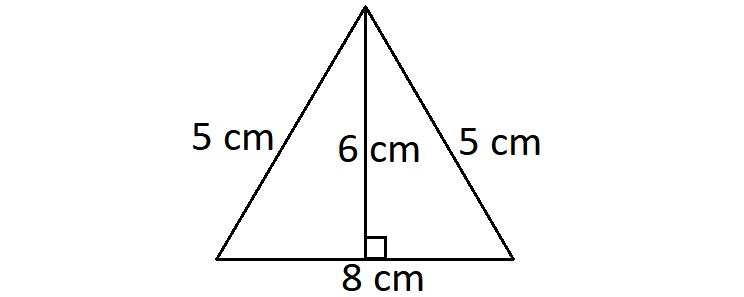
Using the formula for perimeter of the triangle, we have
P = a + b + c
= 5 + 8 + 5
= 18 cm
Using the formula for area of the triangle, we have
A = (1/2) ⋅ b ⋅ h
= (1/2) ⋅ 8 ⋅ 6
= 24 cm2
Kindly mail your feedback to v4formath@gmail.com
We always appreciate your feedback.
©All rights reserved. onlinemath4all.com
Recent Articles
-
Eliminating the Parameter in Parametric Equations
Apr 21, 25 10:37 PM
Eliminating the Parameter in Parametric Equations -
Quadratic Equation Problems with Solutions (Part - 3)
Apr 21, 25 02:37 AM
Quadratic Equation Problems with Solutions (Part - 3) -
Digital SAT Math Problems and Solutions (Part - 147)
Apr 20, 25 08:38 AM
Digital SAT Math Problems and Solutions (Part - 147)