INVERSE FUNCTIONS USING TABLES

Example 1 :

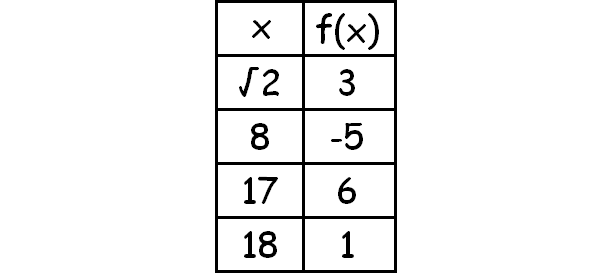
Suppose f is the function whose domain is the four numbers {√2, 8, 17, 18}, with the values of f given in the table shown here in the margin.

(a) What is the range of f ?

(b) Explain why f is a one-to-one function.

(c) What is the table for the function f ⁻¹?

Solution :

(a) In the table above, x represents domain and f(x) represents range. Hence the range of the function is

{3, -5, 6, 1}

(b) From the table above, it is clear that every element of x is associated with an unique element of f(x). Hence it is one to one function.

(c)  From the table above, 

f(√2) = 3, f(8) = -5, f(17) = 6, f(18) = 1

f^-1(3) = √2, f^-1(-5) = 8, f^-1(6) = 17, f^-1(1) = 18

The table for the function f^-1 :

Example 2 :

For f and g are functions, each of whose domain consists of four numbers, with f and g defined by the tables below:

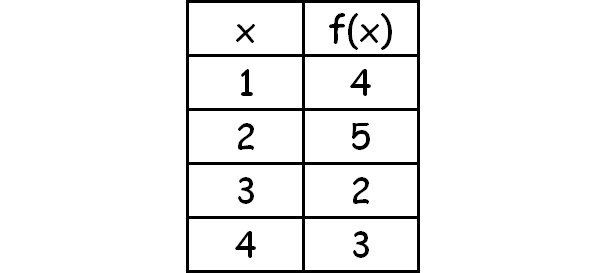
(a) What is the domain of f ?

(b) What is the range of f ?

(c) Sketch the graph of f.

(d) Give the table of values for f⁻¹.

(e) What is the domain of f⁻¹?

(f) What is the range of f⁻¹?

(g) Sketch the graph of f^-1.

(h) Give the table of values for f⁻¹ o f.

(i) Give the table of values for f o f^-1.

Solution :

(a) Domain of f = {1, 2, 3, 4}

(b) Range of f = {2, 3, 4, 5}

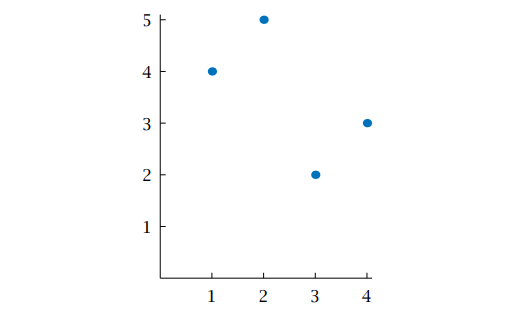
(c) The graph of f consists of all points of the form

(x, f(x))

as x varies over the domain of f . Thus the graph of f, shown below, consists of the four points :

(1, 4), (2, 5), (3, 2), (4, 3)

(d) The table for the inverse of a function is obtained by interchanging the two columns of the table for the function (after which one can, if desired, reorder the rows, as has been done below) :

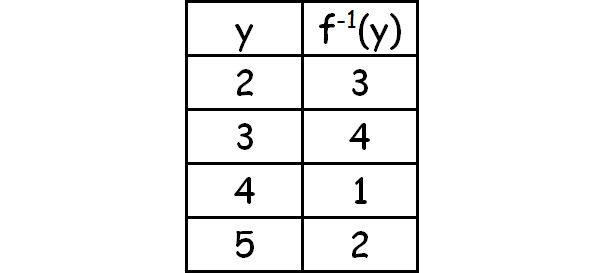
(e) Domain of f^-1 = {2, 3, 4, 5}

(f) Range of f^-1 = {1, 2, 3, 4}

(g) The graph of f^-1 consists of all points of the form

(x, f^-1(x))

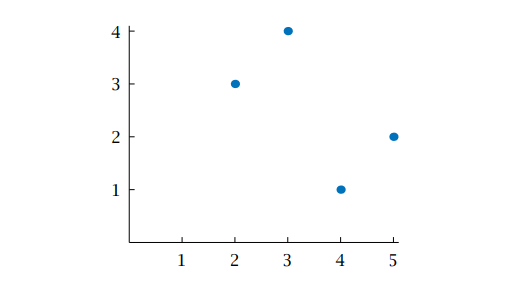
as x varies over the domain of f^-1. Thus the graph of f^-1, shown below, consists of the four points :

(4, 1), (5, 2), (2, 3), (3, 4)

(h)Table of values for f^-1 o f :

(f ⁻¹o f) (1) = f⁻¹[f(1)] = f⁻¹(4) = 1

(f ⁻¹o f) (2) = f⁻¹[f(2)] = f⁻¹(5) = 2

(f ⁻¹o f) (3) = f⁻¹[f(3)] = f⁻¹(2) = 3

(f ⁻¹o f) (4) = f⁻¹[f(4)] = f⁻¹(3) = 4

(i) Table of values for f o f^-1 :

(f o f ⁻¹) (2) = f[(f⁻¹(2)] = f(3) = 2

(f o f ⁻¹) (3) = f[f⁻¹(3)] = f(4) = 3

(f o f⁻¹) (4) = f[f ⁻¹(4)] = f(1) = 4

(f o f ⁻¹) (5) = f[f⁻¹(5)] = f(2) = 5

Example 3 :

The following table gives values of a function f(x) for six inputs 0, 1, 2, 3, 4, and 5.

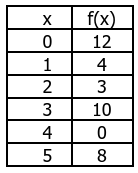
Read the table to find:

Solution :

Example 4 :

If f(x) = (1/8)x - 3, g(x) = x³, h(x) = 2x + 1

Find (f∘g)^-1 (5) ?

Solution :

To evaluate (f∘g)^-1 (x), first let us find (f∘g) (x) and then find its inverse.

(f∘g) (x) = f[g(x)]

= f[x³]

f[g(x)] = (1/8)x³ - 3

Finding inverse of (f∘g) (x) :

Let y = (1/8)x³ - 3

y + 3 = (1/8)x³

x³ = 8(y + 3)

x³ = 8y + 24

x = (8y + 24)^1/3

(f∘g)^-1 (x) = (8x + 24)^1/3

(f∘g)^-1 (5) = (8(5) + 24)^1/3

= (40 + 24)^1/3

= (64)^1/3

= 4

Example 5 :

Find a table of values for each function and its inverse. 

f(x) = 3x + 1

Solution :

f(x) = 3x + 1

When x = 2

f(2) = 3(2) + 1

f(2) = 7

Writing these values as ordered pairs for the function f(x) :

(-4, -11) (-3, -8) (-2, -5) (-1, -2) (0, 1) (1, 4) and (2, 7)

Ordered pairs for the function f^-1(x) :

(-11, -4) (-8, -3) (-5, -2) (-2, -1) (1, 0) (4, 1) and (7, 2)

Example 6 :

Let n = f(t) = 0.25 t – 1.67 represent the number of people (in millions) undergoing laser eye surgery in the year that is t years since 1990.

a) Find & interpret f(10).

b)  Find an equation for f ^–1.

c) Find & interpret f ^–1(3).

d) What is the slope of f ^–1?

What does it mean in the context of this problem ?

Solution :

a) f(t) = 0.25 t – 1.67

f(10) = 0.25 (10) – 1.67

= 2.5 - 1.67

= 0.83

In the year 2000, 83 million people were  undergoing laser eye surgery

b) Finding inverse :

f(t) = 0.25 t – 1.67

Let y = 0.25 t – 1.67

y + 1.67 = 0.25t

(y + 1.67)/0.25 = t

f ^–1(x) = (x + 1.67)/0.25

Find an equation for f ^–1.

c)  f ^–1(3) =  (3 + 1.67)/0.25

= 4.67/0.25

= 18.68

Approximately 19 years

After 19 years in the year of 2009 3 million people were undergoing the laser eye surgery.

d) slope of f ^–1 is 4.

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.