INVERSE OF A QUADRATIC FUNCTION

The general form of a quadratic function is

f(x) = ax² + bx + c

Then, the inverse of the above quadratic function is

f^-1(x)

For example, let us consider the quadratic function

g(x) = x²

Then, the inverse of the quadratic function is g(x) = x² is 

g(x)^-1 = √x

Example 1 :

Find the inverse of the quadratic function and graph it.  

f(x) = x²

Solution :

Replace f(x) by y.

y = x²

Interchange x and y. 

x = y²

y² = x

Solve for y.

Take square root on both sides. 

y = ±√x

Replace y by f^-1(x).

f^-1(x) = ±√x

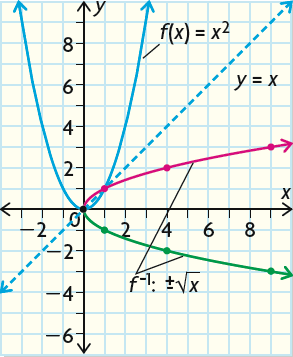
Graphing the inverse of f(x) :

We can graph the original function by plotting the vertex (0, 0). The parabola opens up, because a is positive.

And we get f(1) = 1 and f(2) = 4, which are also the same values of f(-1) and f(-2) respectively.

To graph f^-1(x), we have to take the coordinates of each point on the original graph and switch the x and y coordinates.

For example, (2, 4) becomes (4, 2).

We have to do this because the input value becomes the output value in the inverse, and vice versa.

The graph of the inverse is a reflection of the original  function about the line y = x.

Example 2 :

Find the inverse of the quadratic function and graph it. 

f(x) = 2(x + 3)² - 4

Solution :

Replace f(x) by y.

y = 2(x + 3)² - 4

Interchange x and y. 

x = 2(y + 3)² - 4

Solve for y. 

x + 4 = 2(y + 3)²

(x + 4)/2 = (y + 3)²

Take square root on both sides. 

±√[(x + 4)/2] = y + 3

±√[(x + 4)/2] - 3 = y

y = -3 ± √[(x + 4)/2]

Replace y by f^-1(x).

f^-1(x) = -3 ± √[(x + 4)/2]

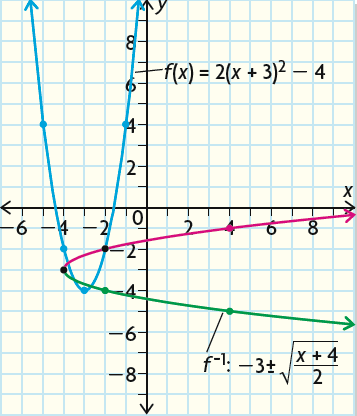
Graphing the inverse of f(x) :

We can graph the original function by plotting the vertex (-3, -4). The parabola opens up, because a is positive.

And we get f(-2) = -2 and f(-1) = 4, which are also the same values of f(-4) and f(-5) respectively.

To graph f^-1(x), we have to take the coordinates of each point on the original graph and switch the x and y coordinates.

For example, (-1, 4) becomes (4, -1).

We have to do this because the input value becomes the output value in the inverse, and vice versa.

Example 3 :

For each quadratic function, complete the square and then determine the equation of the inverse.

a) 𝑓(𝑥) = 𝑥² + 6𝑥 + 15

b) 𝑓(𝑥) = 2 𝑥² + 24𝑥 − 3

Solution :

a) 𝑓(𝑥) = 𝑥² + 6𝑥 + 15

f(x) = 𝑥² + 2(x)(3) + 3² - 3² + 15

f(x) = (𝑥 + 3)² - 3² + 15

f(x) = (𝑥 + 3)² - 9 + 15

f(x) = (𝑥 + 3)² + 6

Let y = (𝑥 + 3)² + 6

Change x = y and y = x

x = (y + 3)² + 6

x - 6 = (y + 3)²

√(x - 6) = y + 3

y = √(x - 6) - 3

f^-1(x) = √(x - 6) - 3

b) 𝑓(𝑥) = 2 𝑥² + 24𝑥 − 3

f(x) = 2 𝑥² + 24𝑥 − 3

= 2[𝑥² + 12𝑥] − 3

= 2[𝑥² + 2(x)(6) + 6² - 6²] - 3

= 2[(𝑥 + 6)² - 6²] - 3

= 2[(𝑥 + 6)² - 36] - 3

= 2(𝑥 + 6)² - 72 - 3

= 2(𝑥 + 6)² - 75

Change x = y and y = x

y = 2(𝑥 + 6)² - 75

y + 75 = 2(𝑥 + 6)²

(𝑥 + 6)² = (1/2) (y + 75)

x + 6 = √(y + 75)/2

x =  1/√2 (√(y + 75)) - 6

Example 4 :

Police use the formula √20 v L to estimate the speed of a car, v, in miles per hour, based on the length, L, in feet, of its skid marks when suddenly braking on a dry, asphalt road.

a) At the scene of an accident, a police officer measures a car's skid marks to be 215 feet long. Approximately how fast was the car traveling?

b) At the scene of an accident, a police officer measures a car's skid marks to be 135 feet long. Approximately how fast was the car traveling?

Solution :

v = √20 L

a)  L = 215 feet

v = √20 (215)

v = 65.57

Speed of the car is 65.57 miles per hour

b) Length = 135 feet

v = √20 (135)

= √2700

v = 51.96

Speed of the car is 51.96 miles per hour

Example 5 :

Determine if the two relations shown are inverses of each other. Justify your conclusion.

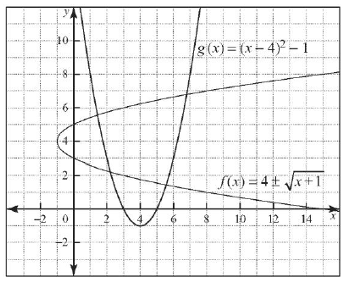
Solution :

g(x) = (x - 4)² - 1

Let y = (x - 4)² - 1

y + 1 = (x - 4)²

x - 4 = √(y + 1)

x = √(y + 1) + 4

Put y = x and x = y

y = √(x + 1) + 4

f^-1(x) = √(x + 1) + 4

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.