INVERSE OPERATIONS

Inverse operations are opposite operations. That is, one reverses the effect of the other.

• Addition and subtraction are inverse operations
• Multiplication and division are inverse operations

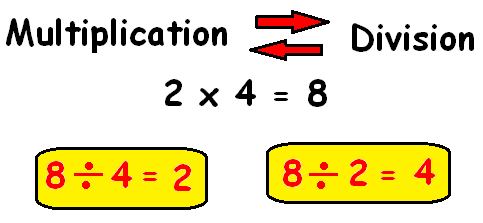
In solving problems in algebra, we use inverse operations to isolate the given variable. 

Example 1 :

Solve for k : 

7k  =  35

Solution :

Here 7 and k are multiplied. 

So, we have to use the inverse operation of multiplication to solve for k. 

Inverse operation of multiplication is division.

7k  =  35

Divide both sides by 7. 

k = 5

Example 2 :

Solve for k ;

k + 7  =  9

Solution :

Here 7 is added to k. 

So, we have to use the inverse operation of addition to solve for k.

Inverse operation of addition is subtraction.

k + 7  =  9

Subtract 7 from each side. 

k  =  2

Example 3 :

Solve for b : 

b/8  =  7

Solution :

Here b is divided by 8. 

So, we have to use the inverse operation of division to solve for b.

Inverse operation of division is multiplication.

b/8  =  7

Multiply each side by 8.

b  =  56

Example 4 :

Solve for m : 

m - 15  =  9

Solution :

Here 15 is subtracted from m. 

So, we have to use the inverse operation of subtraction to solve for b.

Inverse operation of subtraction is addition.

m - 15  =  9

Add 15 to each side. 

 m  =  24

Example 5 :

Solve for z : 

z + 17  =  23

Solution :

Here 17 is added with z. 

So, we have to use the inverse operation of addition to solve for k.

Inverse operation of addition is subtraction.

z + 17  =  23

Subtract 17 from each side.

z  =  6

Example 6 :

Solve for x : 

2x + 5  =  23 

Solution :

Here 5 is added to 2x. 

So, we have to use the inverse operation of addition to solve for 2x.

Inverse operation of addition is subtraction.

2x + 5  =  23

Subtract 5 from each side. 

 2x  =  18 

Here 2 and x are multiplied.

Then, we have to use the inverse operation of multiplication to solve for x.

Inverse operation of multiplication is division. 

2x  =  18

Divide each side by 2.

x  =  9

Example 7 :

Solve for p :

2p - 7  =  3 

Solution :

Here 7 is subtracted from p. 

So, we have to use the inverse operation of subtraction to solve for 2x.

Inverse operation of subtraction is addition.

2p - 7  =  3

Add 7 to each side.

2p  =  10 

Here 2 and p are multiplied.

Then, we have to use the inverse operation of multiplication to solve for x.

Inverse operation of multiplication is division. 

2p  =  10

Divide each side by 2.

p  =  5

Example 8 :

Solve for r : 

(r - 6)/2  =  3

Solution :

Here (r - 6) is divided by 2.

So, we have to use the inverse operation of division to solve for (r - 6).

Inverse operation of division is multiplication.

(r - 6)/2  =  3

Multiply each side by 2.

r - 6  =  6 

Here 6 is subtracted from r.

Then, we have to use the inverse operation of subtraction to solve for r.

Inverse operation of subtraction is addition. 

r - 6  =  6

Add 6 to each side.

r  =  12

Example 9 :

Solve for p : 

(p/3) - 4  =  0 

Solution :

Here 4 is subtracted from (p/3).

So, we have to use the inverse operation of subtraction to solve for (p/3).

Inverse operation of subtraction is addition.

(p/3) - 4  =  0

Add 4 to each side.

p/3  =  4

Here p is divided by 3. 

Then, we have to use the inverse operation of division to solve for p.

Inverse operation of division is multiplication. 

p/3  =  4

Multiply each side by 3.

p  =  12

Example 10 :

Solve for m : 

10 - 3m  =  -5

Solution :

10 - 3m  =  -5

Add 3m to each side. 

10  =  -5 + 3m

Add 5 to each side.

15  =  3m

Divide each side by 3.

5  =  m

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.