INVERSES OF SIN COS AND TAN

Inverses of sin, cosine and tangent functions takes the ratio of corresponding functions and gives the angle measure θ.

Trigonometric Ratio Table

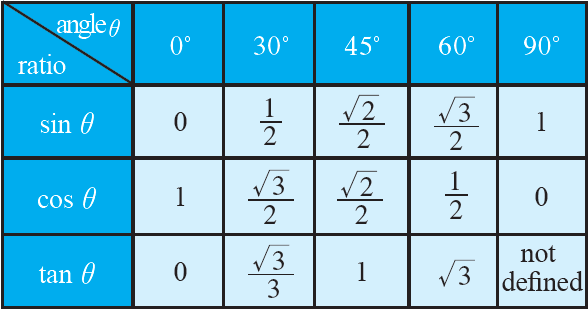
From the trigonometric ratio table above, we have

sin0° = cos90° = 0

sin90° = cos0° = 1

sin30° = cos60° = 1/2

sin60° = cos30° = √3/2

sin45° = cos45° = √2/2

sin0° = tan0° = 0

Examples 1-5 : If θ is an acute angle, find the value of θ in degrees.

Example 1 :

sinθ = 1/2

Solution :

sinθ = 1/2

θ = sin^-1(1/2) ----(1)

From the table above, we have

sin30° = 1/2

30° = sin^-1(1/2) ----(2)

From (1) and (2),

θ = 30°

Example 2 :

tanθ = √3

Solution :

tanθ = √3

θ = tan^-1(√3) ----(1)

From the table above, we have

tan60° = √3

60° = tan^-1(√3) ----(2)

From (1) and (2),

θ = 60°

Example 3 :

cosθ = √2/2

Solution :

cosθ = √2/2

θ = cos^-1(√2/2) ----(1)

From the table above, we have

45° = cos^-1(√2/2) ----(2)

From (1) and (2),

θ = 45°

Example 4 :

sinθ = √2/2

Solution :

sinθ = √2/2

θ = sin^-1(√2/2) ----(1)

From the table above, we have

sin45° = √2/2

45° = sin^-1(√2/2) ----(2)

From (1) and (2),

θ = 45°

Example 5 :

cosθ = √3/2

Solution :

cosθ = √3/2

θ = cos^-1(√3/2) ----(1)

From the table above, we have

cos30° = √3/2

30° = cos^-1(√3/2) ----(2)

From (1) and (2),

θ = 30°

Examples 6-10 : If θ is an acute angle, find the value of θ in radians.

Example 6 :

sinθ = √3/2

Solution :

sinθ = √3/2

θ = sin^-1(√3/2) ----(1)

From the table above, we have

sin60° = √3/2

60° = sin^-1(√3/2) ----(2)

From (1) and (2),

θ = 60°

To convert degrees to radians, multiply by π/180°.

θ = 60° ⋅ (π/180°)

θ = π/3

Example 7 :

cosθ = 1/2

Solution :

cosθ = 1/2

θ = cos^-1(1/2) ----(1)

From the table above, we have

cos60° = 1/2

60° = cos^-1(1/2) ----(2)

From (1) and (2),

θ = 60°

To convert degrees to radians, multiply by π/180°.

θ = 60° ⋅ (π/180°)

θ = π/3

Example 8 :

tanθ = √3/3

Solution :

tanθ = √3/3

θ = tan^-1(√3/3) ----(1)

From the table above, we have

tan30° = √3/3

30° = tan^-1(√3/3) ----(2)

From (1) and (2), 

θ = 30°

To convert degrees to radians, multiply by π/180°.

θ = 30° ⋅ (π/180°)

θ = π/6

Example 9 :

tanθ = 1

Solution :

tanθ = 1

θ = tan^-1(1) ----(1)

From the table above, we have

45° = tan^-1(1) ----(2)

From (1) and (2),

θ = 45°

To convert degrees to radians, multiply by π/180°.

θ = 45° ⋅ (π/180°)

θ = π/4

Example 10 :

tanθ = 1/0

Solution :

tanθ = 1/0

θ = tan^-1(1/0) ----(1)

From the table above, we have

tan90° = not defined

tan90° = 1/0

 90° = tan-1(1/0) ----(2)

From (1) and (2),

θ = 90°

To convert degrees to radians, multiply by π/180°.

θ = 90° ⋅ (π/180°)

θ = π/2

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.