JUSTIFYING ANGLE RELATIONSHIPS

A transversal is a line that intersects two lines in the same plane at two different points. Transversal and the two lines form eight angles. 

In this section, you will learn how to justify the relationships between the eight angles. 

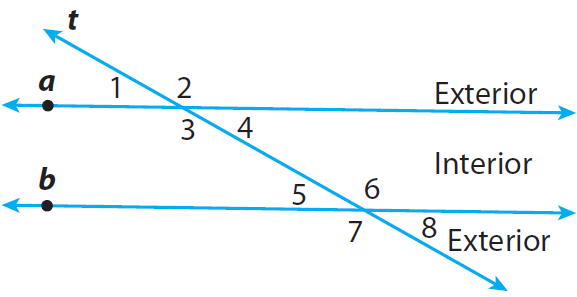
Corresponding Angles : 

Angles lie on the same side of the transversal t, on the same side of lines a and b.

Example : ∠ 1 and ∠ 5

Alternate Interior Angles :

Angles are nonadjacent angles that lie on opposite sides of the transversal t, between lines a and b.

Example : ∠ 3 and ∠ 6

Alternate Exterior Angles :

Angles lie on opposite sides of the transversal t, outside lines a and b. 

Example : ∠ 1 and ∠ 8

Same-Side Interior Angles :

Angles lie on the same side of the transversal t, between lines a and b.

Example : ∠ 3 and ∠ 5

Solved Problems

Problem 1 :

A transversal cuts the two parallel lines and forms eight angles.  Describe the relationships between the angles in the diagram given below. 

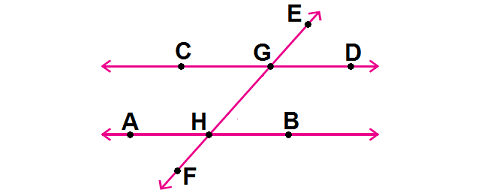
Solution :

Corresponding Angles : 

∠CGE and ∠AHG, ∠DGE and ∠BHG, ∠CGH and ∠AHF, ∠DGH and ∠BHF ; congruent.

Alternate Interior Angles :

∠CGH and ∠BHG, ∠DGH and ∠AHG ; congruent.

Alternate Exterior Angles :

∠CGE and ∠BHF, ∠DGE and ∠AHF ; congruent.

Same-Side Interior Angles :

∠CGH and ∠AHG, ∠DGH and ∠BHG ; supplementary.

Problem 2 : 

In the figure given below,  let the lines l₁ and l₂ be parallel and m is transversal. If ∠F = 65°, using the angle relationships,  find the measure of each of the remaining angles.

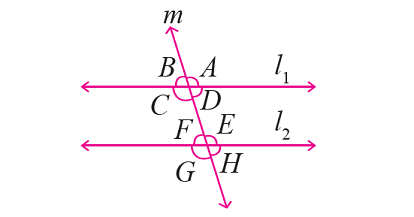
Solution :

From the given figure, 

∠F and ∠H are vertically opposite angles and they are equal. 

Then, ∠H  =  ∠F -------> ∠H  =  65°

∠H and ∠D are corresponding angles and they are equal. 

Then, ∠D  =  ∠H -------> ∠D  =  65°

∠D and ∠B are vertically opposite angles and they are equal. 

Then, ∠B  =  ∠D -------> ∠B  =  65°

∠F and ∠E are together form a straight angle.

Then, we have

∠F + ∠E  =  180°

Plug ∠F  =  65°

∠F + ∠E  =  180°

65° + ∠E  =  180°

∠E  =  115°

∠E and ∠G are vertically opposite angles and they are equal. 

Then, ∠G  =  ∠E -------> ∠G  =  115°

∠G and ∠C are corresponding angles and they are equal. 

Then, ∠C  =  ∠G -------> ∠C  =  115°

∠C and ∠A are vertically opposite angles and they are equal. 

Then, ∠A  =  ∠C -------> ∠A  =  115°

Therefore, 

∠A  =  ∠C  =  ∠E  =  ∠G  =  115°

∠B  =  ∠D  =  ∠F  =  ∠H  =  65°

Problem 3 :

In the figure given below,  let the lines l₁ and l₂ be parallel and t is transversal. Using angle relationships, find the value of x.

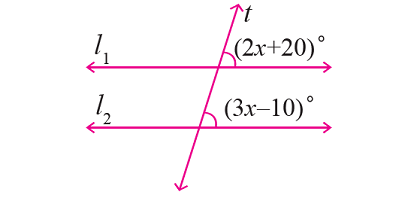
Solution :

From the given figure, 

∠(2x + 20)° and ∠(3x - 10)° are corresponding angles. 

So, they are equal. 

Then, we have

(2x + 20)°  =  (3x - 10)°

2x + 20  =  3x - 10

30  =  x

Problem 4 :

In the figure given below,  let the lines l₁ and l₂ be parallel and t is transversal. Using angle relationships, find the value of x.

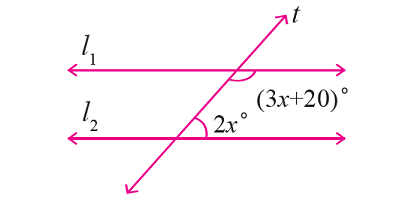
Solution :

From the given figure, 

∠(3x + 20)° and ∠2x° are consecutive interior angles. 

So, they are supplementary. 

Then, we have

(3x + 20)° + 2x°  =  180°

3x + 20 + 2x  =  180

5x + 20  =  180

5x  =  160

x  =  32

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.