JUSTIFYING THE TRIANGLE SUM THEOREM

We can use your knowledge of parallel lines which are cut by a transversal to informally justify the 'Triangle Sum Theorem'.

Follow the steps to informally prove the Triangle Sum Theorem. You should draw each step on your own paper. The figures below are provided for you to check your work.

Step 1 : 

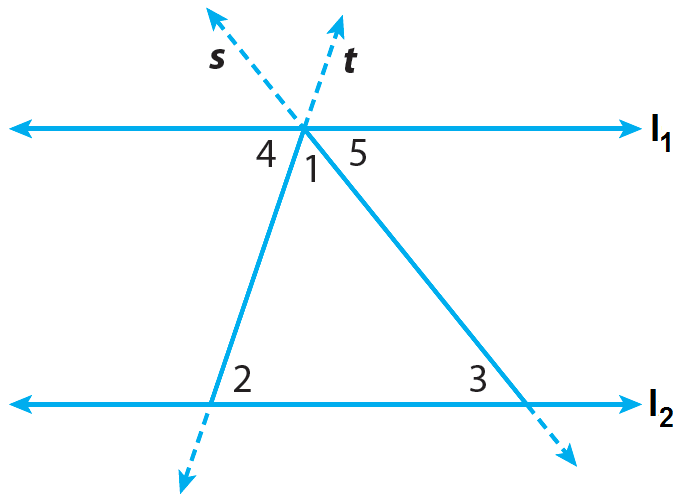
Draw a triangle and label the angles as ∠1, ∠2, and ∠3 as shown.

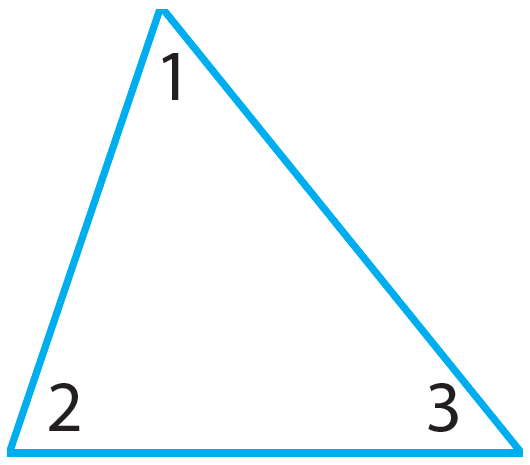
Step 2 : 

Draw line l₁ through the base of the triangle.

Step 3 : 

The Parallel Postulate states that through a point not on a line ℓ, there is exactly one line parallel to line ℓ. Draw line l₂ parallel to line l₁, through the vertex opposite the base of the triangle

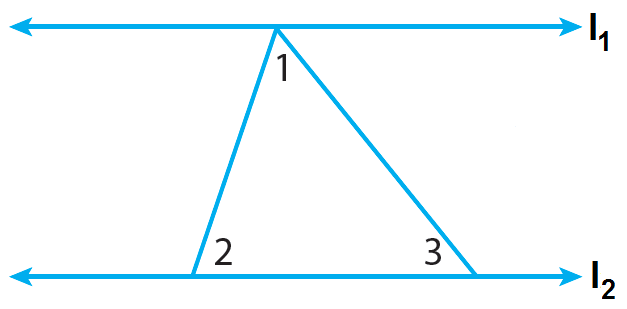
Step 4 : 

Extend each of the non-base sides of the triangle to form transversal s and transversal t. Transversals s and t intersect parallel lines l₁ and l₂.

Label the angles formed by line l₂ and the transversals as ∠4 and ∠5.

Step 5 : 

What do you think about the angles ∠4 and ∠2 ?

∠4 and ∠5 are congruent

Because, when the two parallel lines l₁ and l₂ are cut by the transversal t, ∠4 and ∠5 are alternate interior angles. So, they are congruent.

Step 6 : 

What do you think about the angles ∠5 and ∠3 ?

∠5 and ∠3 are congruent

Because, when the two parallel lines l₁ and l₂ are cut by the transversal s, ∠5 and ∠3 are alternate interior angles. So, they are congruent.

Step 7 : 

The three angles that lie along line b at the vertex of the triangle are ∠1, ∠4, and ∠5. Notice that these three angles lie along a line.

So,  we have

m∠1 + m∠4 + m∠5  =  180°

Step 8 : 

Because angles 2 and 4 are congruent and angles 3 and 5 are congruent, we can replace m∠4 by m∠2 and m∠5 by m∠3 in the equation above.

Then,  we have

m∠1 + m∠2 + m∠3  =  180°

Conclusion :

This shows that the sum of the angle measures in a triangle is always 180°. 

Reflect

1. How can we use the fact that m∠4 + m∠1 + m∠5 = 180°  to show that m∠2 + m∠1 + m∠3  =  180° ?

m∠2  =  m∠4

and

m∠3  =  m∠5

Substituting m∠2 for m∠4 and m∠3 for m∠5 in the equation m∠4 + m∠1 + m∠5  =  180° gives

m∠2 + m∠1 + m∠3  =  180°.

2. Can a triangle have two right angles ? Explain.

No

The sum of the measures of two right angles is 180°. That means the measure of the third angle would be

180° - 180°  =  0°

which is impossible.

3. Describe the relationship between the two acute angles in a right triangle. Explain your reasoning.

No

They are complementary.

The sum of their measures must be

180° - (measure of the right angle)  =  180° - 90°  =  90°

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.