KEY FEATURES OF FUNCTIONS

Following are the key features of functions.

1. Domain and Range

2. x-intercept and y-intercept

3. Positive and Negative intervals

4. Intervals of increasing, decreasing and constant behavior

5. Parent Functions

6. Maxima and Minima

Domain and Range

Domain :

The domain is the set of all possible inputs or x-values. To find the domain of a function, we have to look at the x-axis of the graph.

Determining Domain :

1. Start at the origin.

2. Move along the x-axis until you find the lowest possible x-value. This is your lower bound.

3. Return to the origin.

4. Move along the x-axis until you find your highest possible x-value. This is your upper bound.

Range :

The range is the set of all possible outputs or y-values. To find the range of the graph, we have to look at the y-axis of the graph.

Determining Range :

For the range, do the same thing but move along the y-axis.

x-intercepts and y-intercepts

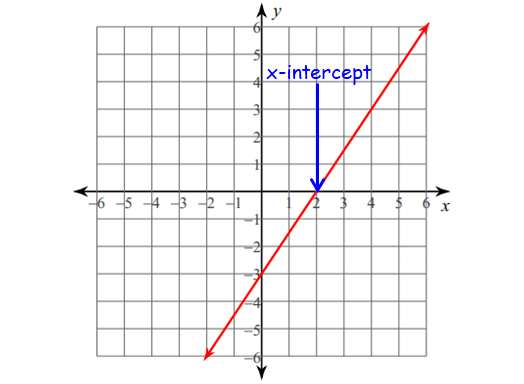
x-intercept :

1. This is where the graph crosses the x-axis.

2. To find it algebraically, set y = 0.

3. Have many names :

• x-intercept
• Roots
• Zeros

Example :

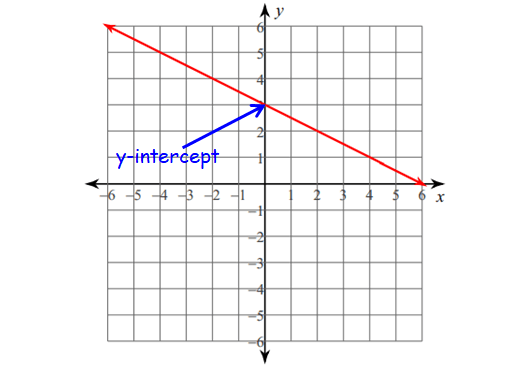
y-intercept :

1. This is where the graph crosses the y-axis.

2. To find it algebraically, set x = 0.

Example :

Positive and Negative Intervals

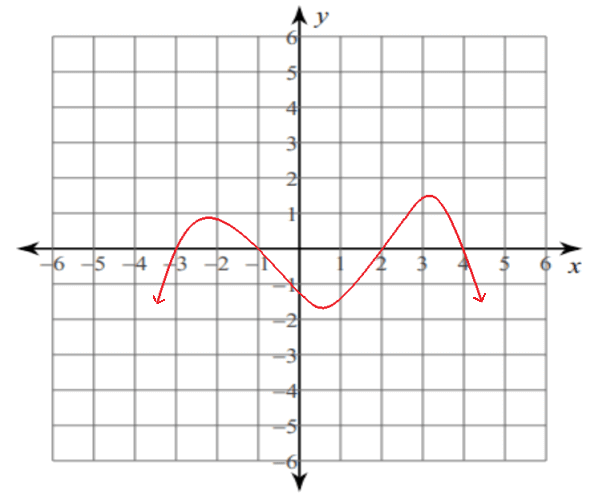
Positive Interval :

In the diagram above, the graph of the function is above the x-axis in the following intervals.

(-3, -1) and (2, 4)

More precisely, y is positive when x ∈ (-3, -1) and (2, 4).

So, the positive intervals for the above graph are

(-3, -1) and (2, 4)

Negative Interval :

In the diagram above, the graph of the function is below the x-axis in the following intervals.

(-∞, -3), (-1, 2) and (4, +∞)

More precisely, y is negative when x ∈ (-∞, -3), (-1, 2) and (4, +∞).

So, the negative intervals for the above graph are

(-∞, -3), (-1, 2) and (4, +∞)

Types of Function Behavior

There are three types of function behavior :

1. Increasing

2. Decreasing

3. Constant

When determining the type of behavior, we always have to move from left to right on the graph.

1. Increasing :

• When x increases, y will also increase
• Direct variation

2. Decreasing :

• When x increases, y will decrease
• Inverse variation

3. Constant :

• When x increases, y will stay the same

Identifying Intervals of Behavior

We use interval notation to represent the behavior of the function.

The interval measures x-values. The type of behavior describes y-values.

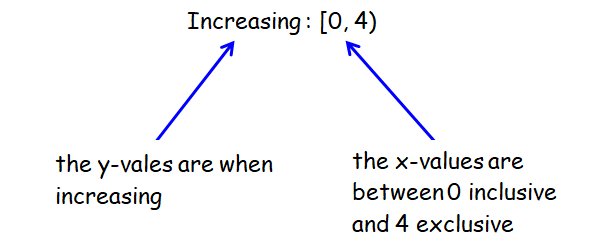
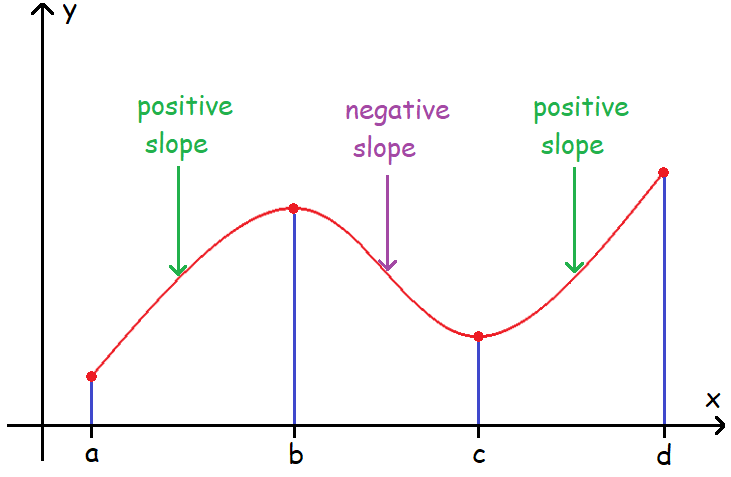
In the diagram above,

* the graph is increasing in the intervals :

(a, b) and (c, d)

* the graph is decreasing in the interval :

(b, c)

Parent Functions and Their Graphs

The most basic for a type of function.

Determines the general shape of the graph (the end behavior).

Baby Functions

Look and behave similarly to their parent functions.

To get a 'baby' function, add, subtract, multiply, and/or divide parent function by constants.

Example :

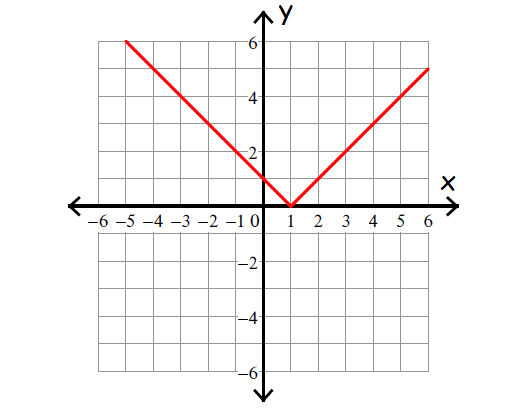
Function Name :

Absolute Value

Parent Function :

f(x)  =  |x|

Baby Function :

f(x)  =  |x - 1|

Identifying Parent Functions

From equations, identify the most important operation :

• Special Operations (Absolute Value)
• Division by x
• Highest Exponent (this includes square roots and cube roots)

Examples :

1. f(x)  =  x2 + 5x + 6

2. f(x)  =  3 / (x + 2)

3. f(x)  =  3|x| + 5 

Maximum (Maxima) and Minimum (Minima) Points

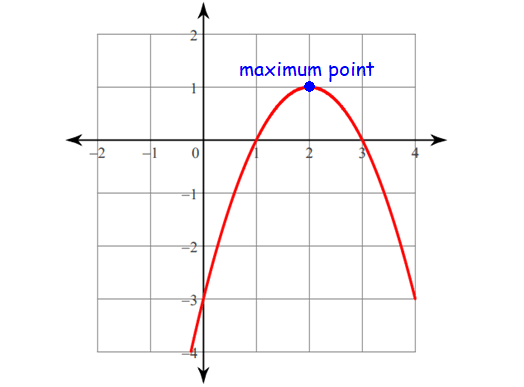
Maximum Point (Maxima) :

Peaks (or hills) are the maximum points.

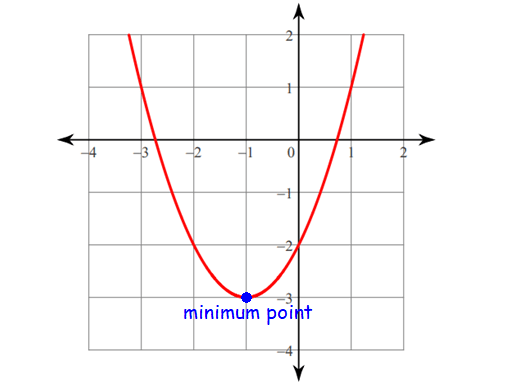
Minimum Point (Minima) :

Valleys are the minimum points.

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.