KITES IN GEOMETRY

A kite is a quadrilateral that has two pairs of consecutive congruent sides, but opposite sides are not congruent.  

Theorems on Kites

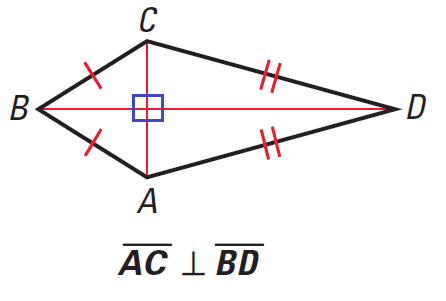
Theorem 1 : 

If a quadrilateral is a kite, then its diagonals are perpendicular. 

It has been illustrated in the diagram shown below. 

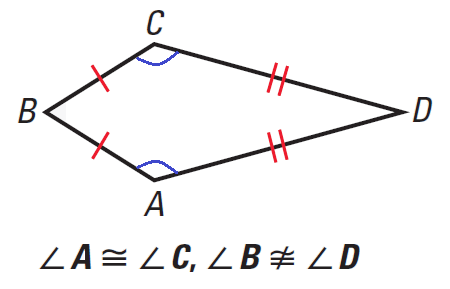
Theorem 2 : 

If a quadrilateral is a kite, then exactly one pair of opposite angles are congruent. 

It has been illustrated in the diagram shown below. 

Kites in Geometry - Practice Problems

Problem 1 : 

In the kite WXYZ shown below, find the length of each side. 

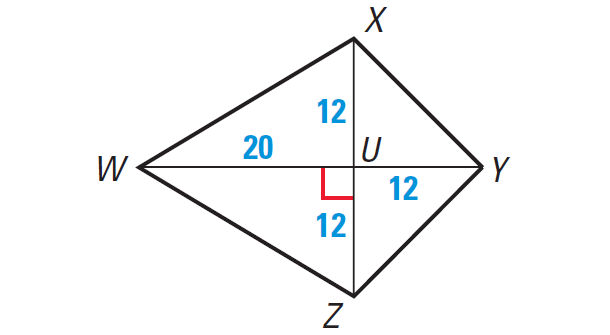
Solution : 

Because WXYZ is a kite, the diagonals are perpendicular. We can use Pythagorean theorem to find the side lengths. 

In the kite WXYZ shown above, let us consider the triangle part WUZ. 

Because the diagonals WY and XZ are perpendicular and they intersect at U, angle U is a right angle. 

So, WUZ is a right triangle. 

By Pythagoren theorem, we have

WZ²  =  WU² + UZ²

Take radical on both sides. 

√WZ²  =  √(WU² + UZ²)

WZ  =  √(20² + 12²)

WZ  =  √(400 + 144)

WZ  =  √544

WZ  ≈  23.32

Similarly, in the right triangle triangle YUZ, we have

YZ²  =  YU² + UZ²

Take radical on both sides. 

√YZ²  =  √(YU² + UZ²)

YZ  =  √(12² + 12²)

YZ  =  √(144 + 144)

YZ  =  √288

YZ  ≈  16.97

We know that a kite is  a quadrilateral that has two pairs of consecutive congruent sides, but opposite sides are not congruent. 

So, in the kite WXYZ shown above, we have

WX  ≅  WZ

YX  ≅  YZ

Hence, we have

WX  =  WZ  ≈  23.32 

YX  =  YZ  ≈  16.97

Problem 2 : 

Find m∠G and m∠J in the diagram shown below. 

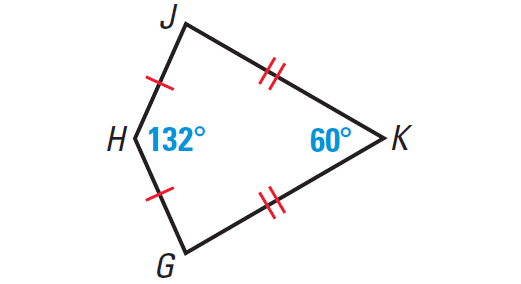
Solution : 

The quadrilateral GHJK shown above has two pairs of consecutive congruent sides, but opposite sides are not congruent. 

So, the quadrilateral GHJK is a kite. 

By theorem 2 above, exactly one pair of opposite angles of a kite are congruent. 

But, in the diagram shown above, the pair of m∠H and m∠K are not congruent.

Then, the pair of m∠G and m∠J must be congruent.

That is, 

m∠G  ≅  m∠J

Let , m∠G  =  m∠J  =  x°

We know that the four angles of a quadrilateral add up to 360°. 

So, we have

m∠G + m∠H + m∠J + m∠K  =  360°

x° + 132° + x° + 60°  =  360°

Simplify.

2x° + 192°  =  360°

Subtract 192° from both sides. 

2x° + 192°  =  360°

2x°  =  168°

Divide both sides by 2. 

x°  =  84°

Hence, we have

m∠G  =  m∠J  =  84°

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.