LEADING COEFFICIENT TEST

Whether the graph of a polynomial rises or falls can be determined by the Leading Coefficient Tests. 

P(x)  =  a_nxⁿ + a_n-1x^n-1 +............. a₁x + a₀

In the above polynomial, n is the degree and a_n is the leading coefficient. 

Case	End Behavior of Graph

When n is odd and a_n is positive

Graph falls to the left and rises to the right 

When n is odd and a_n is negative

Graph rises to the left and falls to the right 

When n is even and a_n is positive

Graph rises to the left and right 

When n is even and a_n is negative

Graph falls to the left and right 

Example 1 :

Find the right-hand and left-hand behaviors of the graph of  

f(x)  =  x⁵ + 2x³ - 3x + 5 

Solution : 

Because the degree is odd and the leading coefficient is positive, the graph falls to the left and rises to the right as shown in the figure.

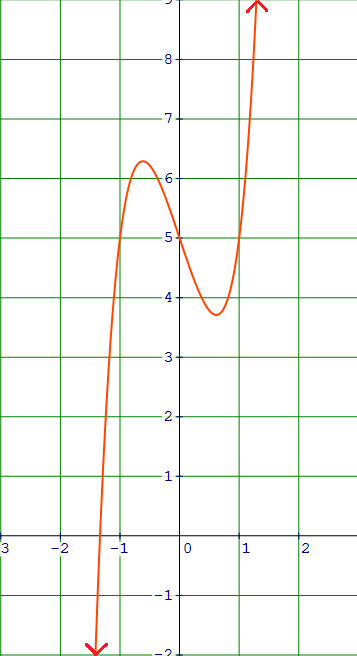
Example 2 :

Determine the end behavior of the graph of the polynomial function below using Leading Coefficient Test. 

P(x)  =  -x³ + 5x

Solution : 

Because the degree is odd and the leading coefficient is negative, the graph rises to the left and falls to the right as shown in the figure.

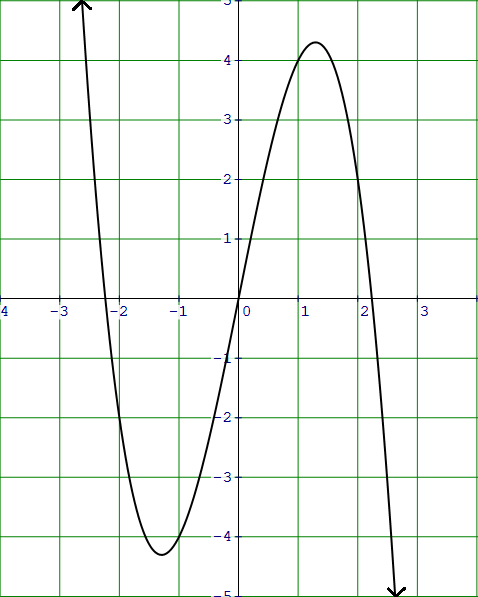
Example 3 :

Determine the end behavior of the graph of the polynomial function below using Leading Coefficient Test. 

P(x)  =  2x² - 2

Solution : 

Because the degree is even and the leading coefficient is positive, the graph rises to the left and right as shown in the figure.

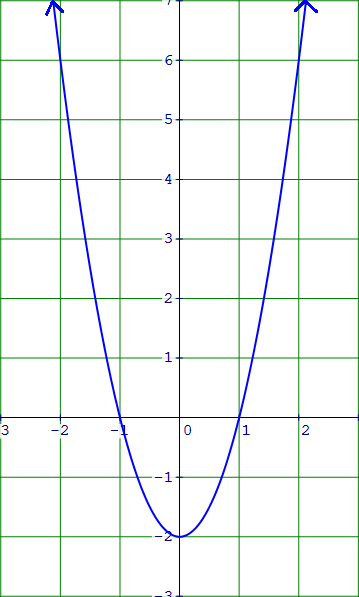
Example 4 :

Determine the end behavior of the graph of the polynomial function below using Leading Coefficient Test. 

P(x)  =  -x² + 1

Solution : 

Because the degree is even and the leading coefficient is negative, the graph falls to the left and right as shown in the figure.

Example 5 :

Describe the right hand and left hand behavior of the graph of each function.

a) f(x) = -x³ + 4x

b) f(x) = x⁴ - 5x² + 4

c) f(x) = x⁵ - x

Solution :

a) f(x) = -x³ + 4x

Degree = 3 (odd)

sign of leading coefficient = negative

Then the end behavior will be the graph will rise in left and falls in right.

b) f(x) = x⁴ - 5x² + 4

Degree = 4 (even)

sign of leading coefficient = positive

Then the end behavior will be, the graph will rise in both left and right.

c) f(x) = x⁵ - x

Degree = 5 (odd)

sign of leading coefficient = positive

Then the end behavior will be, the graph will rise in right and will fall in left.

Example 6 :

Sketch the graph of the function by

a) applying the leading coefficient test

b) Finding the zeroes of the polynomial

c) plotting sufficient solution points

d) drawing continuous curve through the points

i) f(x) = x³ - 25x

ii) g(x) = x⁴ - 9x²

Solution :

a)

Degree = 3

Sign of leading coefficient = positive

End behavior :

The graph will rise right and will fall in left.

b) Finding zeroes :

x³ - 25x = 0

x(x² - 25) = 0

x (x + 5)(x - 5) = 0

x = 0, x = -5 and x = 5

Zeroes are -5, 0 and 5 and x-intercepts are (0, 0) (-5, 0) and (5, 0).

c) Plotting additional points :

(-∞, -5) (-5, 0) (0, 5) and (5,  ∞)

f(x) = x (x + 5)(x - 5)

The polynomial has three distinct real roots, the graph will rise right and will fall in left.

ii) g(x) = x⁴ - 9x²

a)

Degree = 4 (even)

Sign of leading coefficient = positive

End behavior :

The graph will rise both right and left.

b) Finding zeroes :

x⁴ - 9x² = 0

x²(x² - 9) = 0

x² (x + 3)(x - 3) = 0

x = 0, x = -3 and x = 3

Zeroes are -3, 0 and 3 and x-intercepts are (0, 0) (-3, 0) and (3, 0). 0 is the multiplicity of 2.

c) Plotting additional points :

(-∞, -3) (-3, 0)(0, 3) and (3,  ∞)

f(x) = x² (x + 3)(x - 3)

0 has multiplicity of 2 and the other roots are -3 and 3.

Plotting the points,

(-4, 112), (-1, -8), (1, -8) and (4, 112)

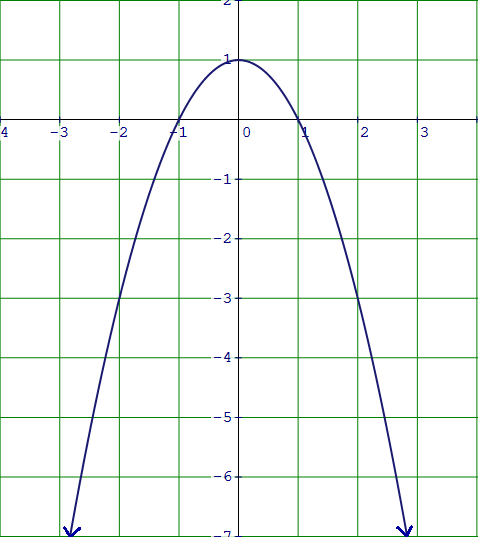
Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.