LEAST COMMON MULTIPLE WORD PROBLEMS

Problem 1 :

Omar is planting trees. He has enough trees to plant 6, 7, or 14 trees in each row. What is the least number of trees Omar could have ?

Solution : 

To find the least number of trees, we have to find the least number that is evenly divisible by 6, 7 and 14. That is the least common multiple of 6, 7 and 14.

Find the least common multiple of 6, 7 and 14.

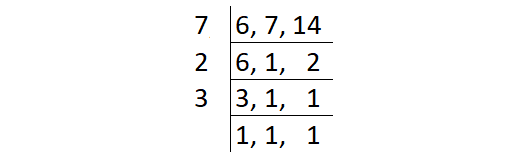
LCM  =  Product of all prime factors

=  7 ⋅ 2 ⋅ 3

=  42

The least number of trees required to plant 6, 7 or 14 tress in each row is 42. 

Problem 2 :

The Line A bus arrives at the bus stop every 25 minutes, and the Line B bus arrives every 15 minutes. They are both at the bus stop right now. In how many minutes will they both be at the bus stop again ?

Solution : 

For example, let the two buses arrive at the bus stop after every 3 minutes  and 4 minutes. 

Then the Line A bus arrives after 3, 6, 9, 12 minutes...... 

Like this, the Line B bus arrives after 4, 8, 12, 16 minutes...... 

If both the buses arrive now, again they will arrive together after 12 minutes. This 12 is the least common multiple (LCM) of 3 and 4.  

The same thing happened in our problem. To find the time, when both the buses are at the bus stop again, we have to find the LCM of (25, 15). 

LCM (25, 15)  =  75

75 minutes  =  1 hour 15 minutes

So, both the buses will be at the bus stop again in 1 hour 15 minutes. 

Problem 3 :

The high school marching band rehearses with either 6 or 10 members in every line. What is the least number of people that can be in the marching band ?

Solution : 

To find the least number of people, we have to find the least number that is evenly divisible by 6 and 10. That is the least common multiple of 6 and 10.

LCM (6, 10)  =  30

The least number of people in the marching band is 30. 

Problem 4 :

Two numbers are in the ratio 4 : 7. If the second number is 35, find their least common multiple.

Solution : 

Because the two numbers are in the ratio 4 : 7, the numbers can be assumed as 4x and 7x.

But, it is given that the second number is 35.

Then, 

7x  =  35

Divide each side by 7.

x  =  5

The first number  =  4(5)  =  20.   

LCM (20, 35)  =  140

So, the least common multiple of the two numbers is 140

Problem 5 :

Two numbers are in the ratio 2 : 3 and their least common multiple is 84. Find the numbers. 

Solution : 

Because the two numbers are in the ratio 2 : 3, the numbers can be assumed as 2x and 3x.

Least common multiple (2x, 3x)  =  6x 

But, it is given that the least common multiple of the two numbers is 84.

Then, 

6x  =  84

Divide each side by 6. 

x  =  14

Substitute x = 8 in 2x and 3x.

2x  =  2(14)  =  28

3x  =  3(14)  =  42

So, the two numbers are 28 and 42.

Problem 6 :

Two numbers are in the ratio 5 : 6 and their sum is 44. Find their least common multiple. 

Solution : 

Because the two numbers are in the ratio 5 : 6, the numbers can be assumed as 5x and 6x.

Then, 

5x + 6x  =  44

11x  =  44

Divide each side by 11. 

x  =  4

Substitute x = 4 in 5x and 6x. 

5x  =  5(4)  =  20

6x  =  6(4)  =  24

The two numbers are 20 and 24.

LCM (20, 24)  =  120

So, the least common multiple of the two numbers is 120.

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.