LEG LEG THEOREM

Leg Leg or LL Theorem is the theorem which can be used to prove the congruence of two right triangles. 

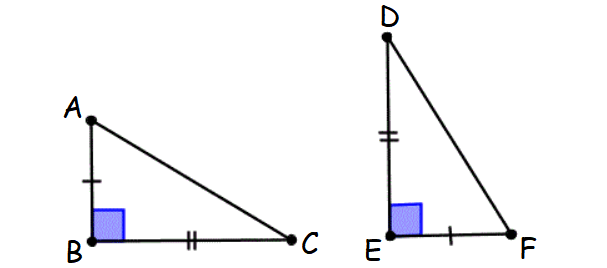
Explanation :

If the legs of one right triangle are congruent to the legs of another right triangle, then the two right triangles are congruent.

This principle is known as Leg-Leg theorem. 

Example :

Check whether two triangles ABC and CDE are congruent.

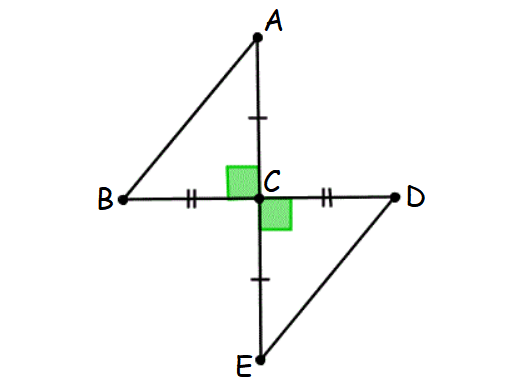
Solution :

(i) Triangle ABC and triangle CDE are right triangles. Because they both have a right angle. 

(i) AC  =  CE (Leg)

(ii) BC  =  CD (Leg)

Hence, the two triangles ABC and CDE are congruent by Leg-Leg theorem. 

Other Triangle Congruence Postulates and Theorems

1. Side-Side-Side (SSS) Congruence Postulate

If three sides of one triangle is congruent to three sides of another triangle, then the two triangles are congruent.

2. Side-Angle-Side (SAS) Congruence Postulate

If two sides and the included angle of one triangle are equal to two sides and the included angle of another triangle, then the two triangles are congruent.

3. Angle-Side-Angle (ASA) Congruence Postulate

If two angles and the included side of one triangle are equal to two angles and the included side of another triangle, then the two triangles are congruent.

4. Angle-Angle-Side (AAS) Congruence Postulate

If two angles and non-included side of one triangle are equal to two angles and the corresponding non-included side of another triangle, then the two triangles are congruent.

5. Hypotenuse-Leg (HL) Theorem

If the hypotenuse and one leg of a right triangle are equal to the hypotenuse and one leg of another right triangle, then the two right triangles are congruent.

6. Leg-Acute (LA) Angle Theorem

If a leg and an acute angle of one right triangle are congruent to the corresponding parts of another right triangle, then the two right triangles are congruent.

7. Hypotenuse-Acute (HA) Angle Theorem

If the hypotenuse and an acute angle of a right triangle are congruent to the hypotenuse and an acute angle of another right triangle, then the two triangles are congruent.

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.