LIKE AND UNLIKE FRACTIONS DEFINITION
Definition of Like Fractions
The fractions which are having the same denominator are called as like fractions.
Example :
⅗, ⁶⁄₅, ⅖, ⁷⁄₅
In all the above fractions, the denominator is same. That is 5.
Definition of Unlike Fractions
The fractions which are having different denominators are called as unlike fractions.
Example :
⅗, ⁶⁄₇, ²⁄₉, ⁷⁄₂
In the above fractions, denominators are different. They are 5, 7, 9 and 2.
The above said stuff is clearly illustrated in the picture shown below.
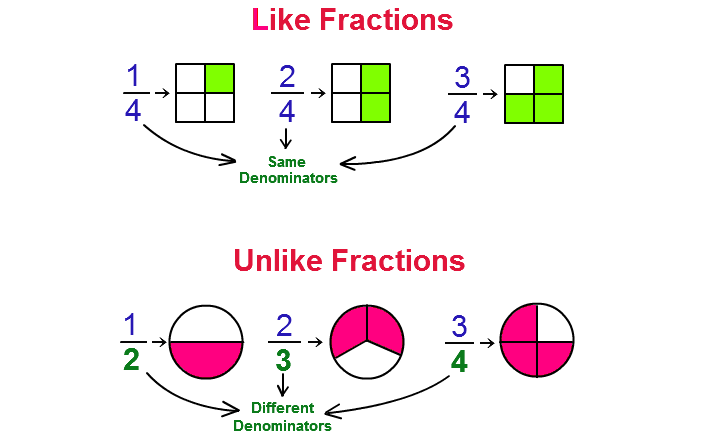
When students want to identify the like fractions and unlike fractions, they have to do a simple work.
That is, they just have to look at the denominators (bottom numbers) of the fractions.
If they are same, they can say that they are like fractions.
In case the denominators are different, they can say that they are unlike fractions.
Adding and Subtracting Fractions
We can understand the difference between like fractions and unlike fractions from the definitions explained above.
The difference between like fractions and unlike fractions will play a key role in adding and subtracting of fractions.
Additition or Subtraction of Two Like Fractions
We have to follow the steps given below to add or subtract two like fractions.
Step 1 :
When two fractions with the same denominator are added or subtracted, take the denominator once.
Step 2 :
Now, add or subtract the numerators and simplify the resulting fraction, if required.
Example :
Find the value of :
⅕ + ⅖
Solution :
= ⅕ + ⅖
The given two fractions have the same denominator. That is 5.
So, take the denominator once and add the numerators.
= ⁽¹ ⁺ ²⁾⁄₅
= ⅗
Additition or Subtraction of Two Unlike Fractions
We can use one of the following methods to add or subtract two fractions with unlike denominators.
1. Cross-Multiplication method
2. LCM (Least Common Multiple) Method.
Cross - Multiplication Method :
In addition or subtraction of two unlike fractions, if the denominators are co-prime or relatively prime, we have to apply this method.
We have to follow the steps explained below in cross multiplication method.
Step 1 :
Multiply the numerator of the first fraction by the denominator of the second fraction.
Step 2 :
Multiply the numerator of the second fraction by the denominator of the first fraction.
Step 3 :
Multiply the denominators of both fractions and take it as common denominator for the results of step 1 and step 2.
Step 4 :
Simplify the result of step 3.
Example :
Let us consider the addition of two fractions given below.
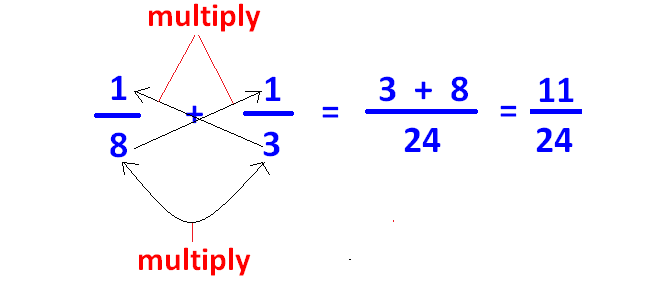
⅛ + ⅓
In the above two fractions, denominators are 8 and 3.
For 8 and 3, there is no common divisor other than 1.
So 8 and 3 are co-prime.
Here, we have to apply cross-multiplication method to add the two fractions 1/8 and 1/3 as shown below.
LCM (Least Common Multiple) Method :
In addition or subtraction of two unlike fractions, if the denominators of the fractions are not co-prime (there is a common divisor other than 1), we have to apply this method.
We have to follow the steps explained below in LCM method.
Step 1 :
Find the least common multiple of the denominators of the given fractions.
Step 2 :
Using the least common multiple found in step 1, make all the fractions as like fractions.
Step 3 :
In like fractions, the denominator of all the fractions will be same. So take the denominator once and simplify the numerators.
Example :
Let us consider the addition of two unlike fractions given below.
⁵⁄₁₂ + ¹⁄₂₀
In the above two fractions, denominators are 12 and 20.
For 12 and 20, if there is at least one common divisor other than 1, then 12 and 20 are not co-prime.
For 12 and 20, we have the following common divisors other than 1.
2 and 4
So 12 and 20 are not co-prime.
In the next step, we have to find the LCM (Least common multiple) of 12 and 20.
12 = 22 x 3
20 = 22 x 5
When we decompose 12 and 20 into prime fractors, we find 2, 3 and 5 as prime factors for 12 and 20.
To get the least vcommon multiple of 12 and 20, we have to take 2, 3 and 5 with maximum powers found above.
So, the least common multiple of 12 and 20 is
= 22 x 3 x 5
= 4 x 3 x 5
= 60
Now, make the denominators of both the fractions as 60 using multiplication.
In (⁵⁄₁₂ + ¹⁄₂₀), to make each denominator as 60, multiply the numerator and denominator of the first fraction by 5 and the second by 3.
Kindly mail your feedback to v4formath@gmail.com
We always appreciate your feedback.
©All rights reserved. onlinemath4all.com
Recent Articles
-
AP Calculus AB Problems with Solutions (Part - 6)
Jan 15, 25 07:19 PM
AP Calculus AB Problems with Solutions (Part - 6) -
Digital SAT Math Problems and Solutions (Part - 100)
Jan 14, 25 12:34 AM
Digital SAT Math Problems and Solutions (Part - 100) -
SAT Math Resources (Videos, Concepts, Worksheets and More)
Jan 14, 25 12:23 AM
SAT Math Resources (Videos, Concepts, Worksheets and More)