LIMIT OF A FUNCTION EXAMPLES WITH ANSWERS

Question 1 :

Evaluate the following limit 

lim  _{x -> 0} √(x² + a²) - a / √(x² + b²) - b

Solution :

  =  lim  _{x -> 0} √(x² + a²) - a / √(x² + b²) - b

We may distribute the limits for the numerator and denominator. 

  =  lim  _{x -> 0} √(x² + a²) - a / lim  _{x -> 0} √(x² + b²) - b

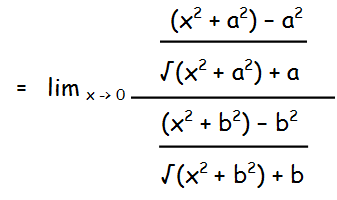
  =  lim x->0 [x²+a²-a²/√(x²+a²)+a)]/[x²+b²-b²/√(x²+b²)+b)] 

  =  lim x->0 [x²/√(x²+a²)+a)]/[x²/√(x²+b²)+b)] 

  =  lim x->0 [x²/√(x²+a²)+a)] ⋅ [√(x²+b²)+b)/x²] 

  =  lim x->0 [√(x²+b²)+b)/√(x²+a²)+a)]

  =  2b/2a

=  b/a

Hence the value of lim  _{x -> 0} √(x² + a²) - a / √(x² + b²) - b is b/a.

Question 2 :

Evaluate the following limit 

lim _{x-> 0}  (2 arc sinx/3x)

Solution :

   =  lim _{x-> 0}  (2 sin^-1x/3x)

  =  (2/3) lim _{x-> 0}  (sin^-1x/x)

  =  2/3

Hence the value of lim _{x-> 0}  (2 arc sinx/3x) is 2/3.

Question 3 :

Evaluate the following limit 

lim _{x-> 0}  (1 – cos x)/x²

Solution :

  =  lim _{x-> 0}  (2 sin²(x/2)/(x²(4/4))

  =  lim _{x-> 0}  (2/4) sin²(x/2)/(x/2)²

  =  lim _{x-> 0}  (2/4) (sin(x/2)/(x/2))²

  =  (1/2) lim _{x-> 0}  (sin(x/2)/(x/2))²

  =  1/2

Hence the value of lim _{x-> 0}  (1 – cos x)/x² is 1/2.

Question 4 :

Evaluate the following limit 

 lim _{x-> 0}  (tan 2x/x)

Solution :

  =  lim _{x-> 0}  (tan 2x/x(2/2))

  =  lim _{x-> 0}  2 (tan 2x/2x)

  =  2 lim _{x-> 0}  (tan 2x/2x)

  =  2

Hence the value of  lim _{x-> 0}  (tan 2x/x) is 2.

Question 5 :

Evaluate the following limit

lim _{x-> 0}  (2^x – 3^x)/x

Solution :

  =  lim _{x-> 0}  (2^x – 1 + 1 – 3^x)/x

  =  lim _{x-> 0}  [(2^x – 1) – (3^x - 1)]/x

  =  [lim _{x-> 0}  (2^x – 1)/x] – [lim _{x-> 0} (3^x - 1)/x]

  =  log 2 – log 3

  =  log (2/3)

Question 6 :

Evaluate the following limit

lim _{x-> 0}  (3^x – 1)/√(x+1) – 1

Solution :

  =  lim _{x-> 0}  ((3^x – 1)/√(x+1) – 1) (√(x+1) + 1 / √(x+1) + 1)

  =  lim _{x-> 0}  ((3^x – 1)/((x+1) – 1) (√(x+1) + 1)

  =  lim _{x-> 0}  ((3^x – 1)/x) (√(x+1) + 1)

  =  lim _{x-> 0}  ((3^x – 1)/x) lim _{x-> 0} (√(x+1) + 1)

  =   log 3 (2)

  =  2 log 3

  =  log 3²

  =  log 9

Hence the value of lim _{x-> 0}  (3^x – 1)/√(x+1) – 1 is log 9.

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.