LINEAR APPROXIMATION OF A FUNCTION OF SEVERAL VARIABLES

Let A = {(x, y) | a < x < b, c < y < d} ⊂ ℝ² , F : A->ℝ and (x₀, y₀)∈A is defined to be

(i) The linear approximation of F at (x₀, y₀) ∈ A is defined to be

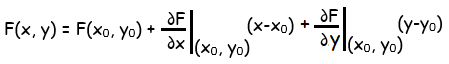
(ii) The differential of F is defined to be

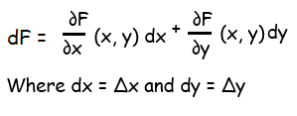
Problem 1 :

If

w(x, y) = x³−3xy+2y²

x, y∈ℝ, find the linear approximation for w at (1,−1) .

Solution :

w(x, y) = x³−3xy+2y²

W at (1, -1)

w(1, -1) = 1³−3(1)(-1)+2(-1)²

= 1 + 3 + 2

= 6

Finding ∂w/∂x :

Differentiate with respect to x.

∂w/∂x = 3x²-3(1)y+0 

∂w/∂x = 3x²-3y

∂w/∂x at(1, -1)  =  6  ---(1)

Finding ∂w/∂y :

Differentiate with respect to y.

∂w/∂y = 0-3xy+2(2y) 

∂w/∂y = -3xy+4y

∂w/∂y at(1, -1)  =  -1  ----(2)

(x-x₀)  ==> (x-1)

(y-y₀)  ==> (y+1)

Applying the formula, we get

=  6 + (x²-3y) at (1, -1)(x-1) + (-3xy+4y) at (1, -1) (y+1)

=  6 + 6(x-1) + (-1) (y+1)

=  6+6x-6-y-1

=  6x-y-1

Problem 2 :

Let z(x, y) = x² y + 3xy⁴, x, y∈ℝ.

Find the linear approximation for z at (2, −1) .

Solution :

z(x, y) = x² y + 3xy⁴

z at (2, -1)

z(x, y) = 2² (-1) + 3[2(-1)⁴]

= -4+6

= 2

Finding ∂z/∂x :

Differentiate with respect to x.

∂z/∂x = 2xy+3(1)y⁴

∂z/∂x = 2xy+3y⁴

When x = 2 and y = -1

= -4+3

= -1

∂z/∂x at(2, -1)  =  -1  ---(1)

Finding ∂z/∂y :

Differentiate with respect to y.

Given : z(x, y) = x² y + 3xy⁴

∂z/∂y = x² (1) + 3x(4y³)

∂z/∂y = x² + 12xy³ 

When x = 2 and y = -1

∂z/∂y = 4-24

=  -20

∂z/∂y at(2, -1)  =  -20  ----(2)

(x-x₀)  ==> (x-2)

(y-y₀)  ==> (y+1)

Applying the formula, we get

= 2 + ∂z/∂x at(2, -1) (x-2) + ∂z/∂y at(2, -1) (y+1)

= 2-1(x-2)-20(y+1)

= 2-x+2-20y-20

= -x-20y-16

= -(x+20y+16)

Problem 3 :

If

v(x, y) = x²-xy+(1/4)y²+7

and x, y∈ℝ. find the differential dv.

Solution :

v(x, y) = x²-xy+(1/4)y²+7

∂v/∂x = 2x-1y+0

∂v/∂x = 2x-y

∂v/∂y = 0-x(1)+(1/4)(2y)+0

∂v/∂y = -x+(y/2)

dv = (2x-y)dx + (-x+(y/2)) dy

Problem 4 :

Let

W(x, y, z) = x²-xy+3sinz and x, y, z ∈ ℝ.

Find the linear approximation at (2, -1, 0).

Solution :

W(x, y, z) = x²-xy+3sinz

W at (2, -1, 0) :

= 2²-2(-1)+3sin(0)

= 4+2+3(0)

= 6

Finding ∂W/∂x :

∂w/∂x = 2x-(1)y+0

∂w/∂x = 2x-y

∂w/∂x at(2, -1, 0) = 2(2)-(-1)

= 4+1

= 5

Finding ∂W/∂y :

 x²-xy+3sinz

∂w/∂y = 0-x(1)+0

∂w/∂y = -x

∂w/∂y at(2, -1, 0) = -2

Finding ∂W/∂z :

 x²-xy+3sinz

∂w/∂z = 0-0+3cosz

∂w/∂z at(2, -1, 0) = 3cos0

=  3

(x-x₀) = (x-2)

(y-y₀) = (y+1)

(z-z₀) = (z-0)

By applying the formula, we get

= 6+5(x-2)-2(y+1)+3(z-0)

= 6+5x-10-2y-2+3(z-0)

= 5x-2y+3z-6

Problem 5 :

Let V (x, y, z) = xy + yz + zx, x, y, z ∈ ℝ. Find the differential dV .

Solution :

Finding ∂V/∂x :

V (x, y, z) = xy + yz + zx

= 1y+0+z(1)

= y+z

Finding ∂V/∂y :

= x(1)+(1)z+0

= x+z

Finding ∂V/∂z :

= 0+y(1)+(1)x

= y+x

dV = (y+z)dx+(x+z)dy+(y+x)dz

Apart from the stuff given above, if you need any other stuff in math, please use our google custom search here.

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.