LINEAR INEQUALITIES IN ONE VARIABLE WITH FRACTIONS

Example 1 :

Solve the following linear inequality :

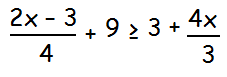
Solution :

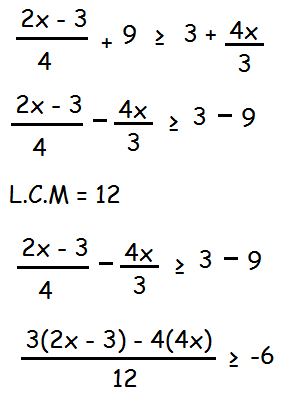
(6x - 9 - 16x) / 12  ≥  - 6

(-10 x - 9) / 12  ≥  - 6 

Multiply each side by 12. 

[(-10 x - 9)/12] x 12 ≥ -6 x 12

-10x - 9 ≥ -72

Add 9 on both sides

-10 x - 9 + 9 ≥ -72 + 9

-10x ≥ -63

Divide by -10  on both sides

-10x/(-10) ≤ -63/(-10)

x ≤ 63/10

x ∈ (-∞, 63/10]

Hence, the solution set of the given inequality is

(-∞, 63/10]

Example 2 :

Solve the following linear inequality 

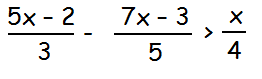
Solution :

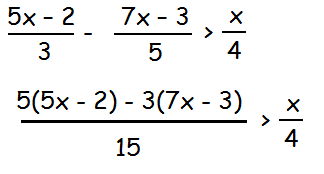
(25x - 10 - 21x + 9)/15 > x/4

(4x - 1)/15 > x/4

Multiply by 15 on both sides

4x - 1 > (x/4) x 15

4x - 1 > 15x/4

Multiply by 4 on both sides

4(4x - 1) > 15x

16x - 4 > 15x 

Subtract 15x on both sides

16x - 15x  - 4 > 15x - 15x

x - 4 > 0

Add 4 on both sides

x - 4 + 4 > 0 + 4

x > 4

x ∈ (4, ∞)

Hence, the solution set of the given inequality is

(4, ∞)

Example 3 :

Solve the following linear inequality 

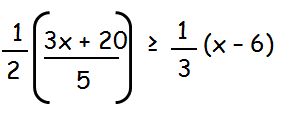
Solution :

(3x + 20)/10 ≥ (x - 6)/3

Multiply by 10 on both sides

3x + 20  ≥ 10(x - 6)/3

Multiply by 3 on both sides

3(3x + 20) ≥ 10(x - 6)

9x + 60 ≥ 10x - 60

Subtract 10 on both sides

9x - 10x + 60 ≥ 10x - 10x - 60

-x + 60 ≥ - 60

Subtract 60 on both sides

-x + 60 - 60 ≥ - 60 - 60

-x ≥ - 120

Divide by (-1) on both sides

x ≤ 120

x ∈ (-∞, 120]

Hence, the solution set of the given inequality is 

(-∞, 120]

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.