LINEAR INEQUALITIES WORKSHEET FOR GRADE 11

1)  Represent the following inequalities in the interval notation:

(i) x ≥ −1 and x < 4 (ii) x ≤ 5 and x ≥ −3

(iii) x < −1 or x < 3 (iv) −2x > 0 or 3x − 4 < 11.   Solution

2)  Solve 23x < 100 when

(i) x is a natural number, (ii) x is an integer.  Solution

3)  Solve −2x ≥ 9 when

(i) x is a real number, (ii) x is an integer, (iii) x is a natural number.  Solution

4. Solve

Solution

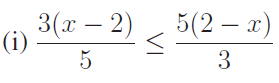
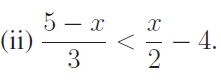
5)  To secure A grade one must obtain an average of 90 marks or more in 5 subjects each of maximum 100 marks. If one scored 84, 87, 95, 91 in first four subjects, what is the minimum mark one scored in the fifth subject to get A grade in the course?      Solution

6)  A manufacturer has 600 litres of a 12 percent solution of acid. How many litres of a 30 percent acid solution must be added to it so that the acid content in the resulting mixture will be more than 15 percent but less than 18 percent?       Solution

7)  Find all pairs of consecutive odd natural numbers both of which are larger than 10 and their sum is less than 40. 

Solution 

8)  A model rocket is launched from the ground. The height h reached by the rocket after t seconds from lift off is given by h(t) = −5t² + 100t, 0 ≤ t ≤ 20. At what time the rocket is 495 feet above the ground?

Solution 

9)  A plumber can be paid according to the following schemes: In the first scheme he will be paid rupees 500 plus rupees 70 per hour, and in the second scheme he will paid rupees 120 per hour. If he works x hours, then for what value of x does the first scheme give better wages?

Solution 

10)  A and B are working on similar jobs but their annual salaries differ by more than Rs 6000. If B earns rupees 27000 per month, then what are the possibilities of A’s salary per month?

Solution 

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.