LINEAR MODEL WORD PROBLEMS WORKSHEET

Problem 1 :

The cost of a school banquet is $95 plus $15 for each person attending. Write an equation that gives total cost as a function of the number of people attending. What is the cost for 77 people?

Solution

Problem 2 :

In 1980 the average price of a home in Brainerd County was $97,000. By 1986 the average price of a home was $109,000. Write a linear model for the price of a home, P, in Brainerd County as a function of the year, t. Let t = 0 correspond to 1980.

Solution

Problem 3 :

Roman paid $150 to join a handball club. He pays an additional $15 every time he uses one of the club's handball courts. Write an equation that describes Roman's total cost for playing handball as a function of the number of times he plays.

Let C = the total cost and n = the number of times he plays.

Solution

Problem 4 :

A sunflower in Julia Rosario's garden was 12 centimeters tall when it was first planted. Since then, it has grown approximately 0.6 centimeters per day. Write an equation expressing the sunflower's height, H, in terms of the number of days, d, since it was planted.

Solution

Problem 5 :

Billy plans to paint baskets. The paint costs $14.50. The baskets cost $7.25 each. Write an equation that gives the total cost as a function of the number of baskets made. Determine the cost of four baskets.

Solution

Problem 6 :

A real estate sales agent receives a salary of $250 per week plus a commission of 2% of sales. Write an equation that gives the weekly income y in terms of sales x.

Solution

Problem 7 :

If a large factory sells its new gadgets for $5 each, it can sell 1050 per month, and if it sells the same gadgets for $9, it will sell 900 per month. Assuming the relationship between price and sales is linear, predict the monthly sales of gadgets to the nearest whole number if the price is $12.

Solution

Problem 8 :

The graph for a stable that charges a $20 flat fee plus $10 per hour for horseback riding is shown below.

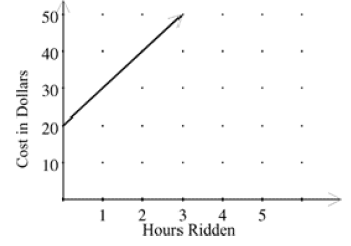
How will the graph change if the stable changes its charges to a flat fee of $45 plus $30 per hour?

Solution

Problem 1 :

A park charges $10 for adults and $5 for kids. How many many adults tickets and kids tickets were sold, if a total of 548 tickets were sold for a total of $3750 ? 

Problem 2 :

A manufacturer produces 80 units of a product at $22000 and 125 units at a cost of $28750. Assuming the cost curve to be linear, find the equation of the line and then use it to estimate the cost of 95 units.

Problem 3 :

A trader has 100 units of a product. A sells some of the units at $6 per unit and the remaining units at $8 per units. He receives a total of $660 for all 100 units. Find the number units sold in each category. 

Problem 4 :

The wages of 8 men and 6 boys amount to $33. If 4 men earn $4.50 more than 5 boys, determine the wages of each man and boy. 

Problem 5 :

Sum of incomes of A and B is $2640. If B's income is 20% more than A, find the income of A and B. 

Problem 6 :

A trader gains one third of the cost price as profit on a product and one fourth of the cost price as profit on other product. Total profit earned on these two products is $43.  The sum of the cost prices of two products is $150. Find the cost price of each product. 

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.