LINEAR PAIR POSTULATE WORKSHEET

Problem 1 :

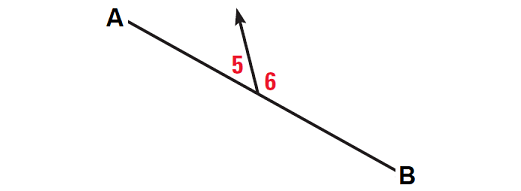
In the diagram shown below, AB is a straight line. Find the sum of the angle measures 5 and 6.

Problem 2 :

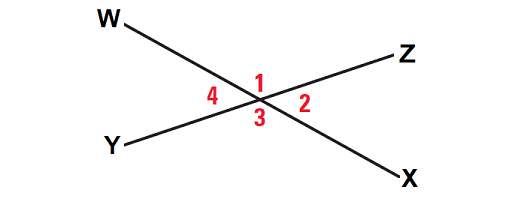
In the diagram shown below, WX and YZ are two straight lines intersecting. Find the sum of the following pairs of angle measures :

angle 1 and angle 2

angle 2 and angle 3

angle 3 and angle 4

angle 4 and angle 1

Problem 3 :

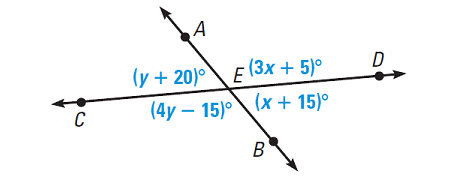
In the diagram shown below, solve for x and y. Then, find the angle measures. 

Problem 4 :

In the stair railing shown at the right, m∠6 has a measure of 130°. Find the measures of the other three angles.

1. Answer :

In the given diagram, since AB is a straight line, ∠5 and  ∠6 form a linear pair.

So, they are supplementary. 

m∠5 + m∠6  =  180°

Sum of the angle measures 5 and 6 is 180°.

2. Answer :

In the given diagram, since WX and YZ are straight lines, the following pairs of angle measures are linear pairs. 

angle 1 and angle 2

angle 2 and angle 3

angle 3 and angle 4

angle 4 and angle 1

So, 

m∠1 + m∠2  =  180°

m∠2 + m∠3  =  180°

m∠3 + m∠4  =  180°

m∠4 + m∠1  =  180°

3. Answer :

Use the fact that the sum of the measures of angles that form a linear pair is 180°. 

Solving for x :

∠AED and ∠DEB form a linear pair.

m∠AED + m∠DEB  =  180°

Substitute m∠AED = (3x + 5)° and m∠DEB = (x + 15)°.

(3x + 5)° + (x + 15)°  =  180°

Simplify.

4x + 20  =  180

Subtract 20 from each side.  

4x  =  160

Divide each side by 4.

x  =  40

Solving for y :

∠AEC and ∠CEB form a linear pair. 

m∠AEC + m∠CEB  =  180°

Substitute m∠AEC = (y + 20)° and m∠CEB = (4y - 15)°.

(y + 20)° + (4y - 15)°  =  180°

Simplify.

5y + 5  =  180

Subtract 5 from each side.  

5y  =  175

Divide each side by 5.

y  =  35

Use substitution to find the angle measures :

m∠AED  =  (3x + 5)°  =  (3 • 40 + 5)°  =  125°

m∠DEB  =  (x + 15)°  =  (40 + 15)°  =  55°

m∠AEC  =  ( y + 20)°  =  (35 + 20)°  =  55°

m∠CEB  =  (4y - 15)°  =  (4 • 35 - 15)°  =  125°

So, the angle measures are 125°, 55°, 55°, and 125°. Because the vertical angles are congruent, the result is reasonable.

4. Answer :

In the diagram above, ∠5 and ∠6 form a linear pair.

m∠5 + m∠6  =  180°

Substitute m∠6 = 130°.

m∠5 + 130  =   180°

Subtract 130° from both sides.

m∠5  =   50°

∠6 and ∠7 also form a linear pair. So, it follows that  

m∠7  =  50° 

∠7 and ∠8 also form a linear pair. So, it follows that 

m∠8  =  130°

Therefore, 

m∠5  =  50°

m∠7  =  50°

m∠8  =  130°

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.