LINES AND ANGLES IN SAT MATH

Problem 1 :

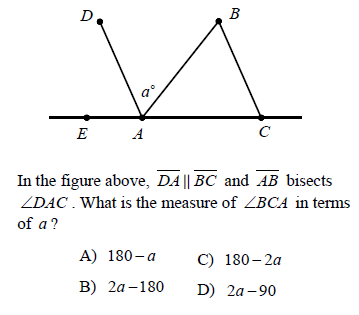
Solution :

Line segment AB is bisecting the ∠DAC.

∠DAB  =  ∠BAC  =  a

∠EAD + ∠DAB + ∠BAC  =  180

∠EAD + a + a  =  180

∠EAD  =  180 - 2a

∠EAD  =  ∠ACB  =  Corresponding angles

∠ACB  =  180 - 2a

Problem 2 :

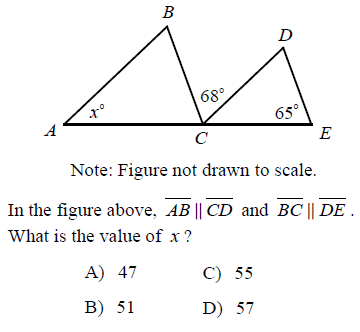
Solution :

Since BC and DE are parallel,

∠ACB  =  65  =  ∠DEC (Corresponding angles)

Since AB and CD are parallel,

∠BAC  =  x  =  ∠DCE (Corresponding angles)

∠ACB + ∠CD + ∠DCE  =  180

65 + 68 + x  =  180

133 + x  =  180

x  =  180 - 133

x  =  47

Problem 3 :

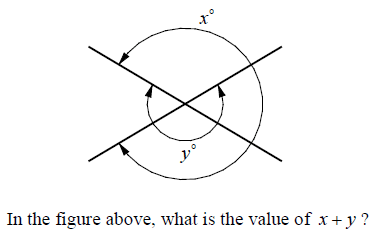
Solution :

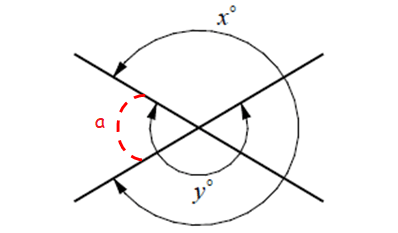
From the picture above,

y  =  180 + a ----(1)

a + x  =  360

x  =  360 - a ----(2)

(1) + (2) :

x + y  =  360 - a + 180 + a

x + y  =  540

Problem 4 :

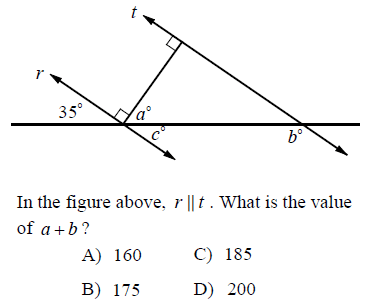
Solution :

Form the given picture, we know that 

a + c  =  90

c = 35 (Vertically opposite angles)

a + 35  =  90

a  =  90 - 35

a  =  55

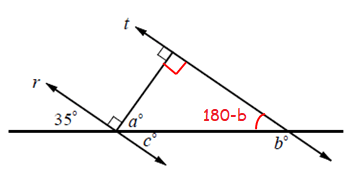
In the triangle,

a + 90 + 180 - b  =  180

a + 270 - b  =  180

55 + 270 - b  =  180

325 - b  =  180

b  =  325 - 180

b  =  145

a + b  =  55 + 145

a + b  =  200

Problem 5 :

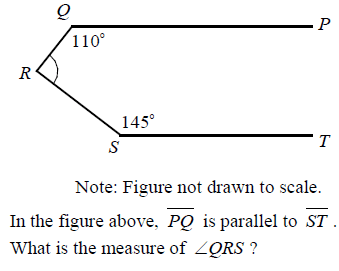
Solution :

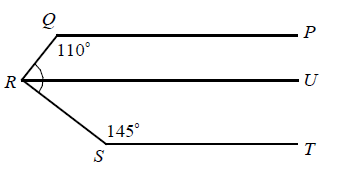
∠QRU + ∠RQP  =  180

∠QRU + 110  =  180

∠QRU  =  70 ----(1)

∠TSR + ∠SRU  =  180

145 + ∠SRU  =  180

∠SRU  =  35 ----(2)

(1) + (2) :

∠QRS  =  ∠QRU + ∠SRU

∠QRS  =  70 + 35

∠QRS  =  105

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.