LINES AND ANGLES PROBLEMS WITH SOLUTIONS FOR SAT

Problem 1 :

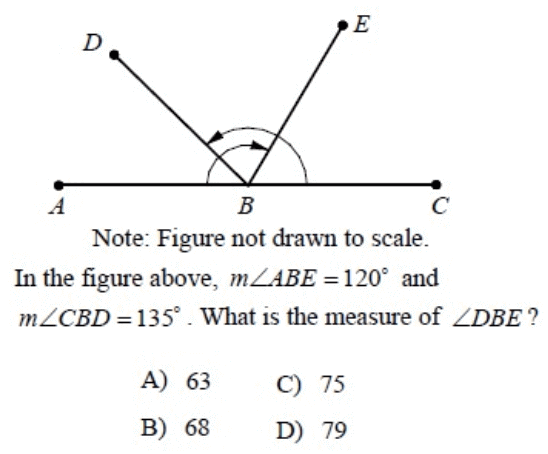
Solution :

∠ABE = 120°

∠ABD + ∠DBE = 120° ----(1)

∠CBD = 135°

∠CBE + ∠EBD = 135°

∠CBE + ∠DBE = 135°  ----(2)

(2) - (1) :

(∠CBE + ∠DBE) - (∠ABD + ∠DBE) = 135° - 120°

∠CBE - ∠ABD = 15°

∠CBE = 15° + ∠ABD

From the figure, we know that

∠ABE + ∠EBC = 180°

120° + 15° + ∠ABD = 180°

∠ABD = 180° - 135°

∠ABD = 45°

By applying the value of ∠ABD in (1), we get

45 + ∠DBE = 120°

∠DBE = 120° - 45°

∠DBE = 75°

Problem 2 :

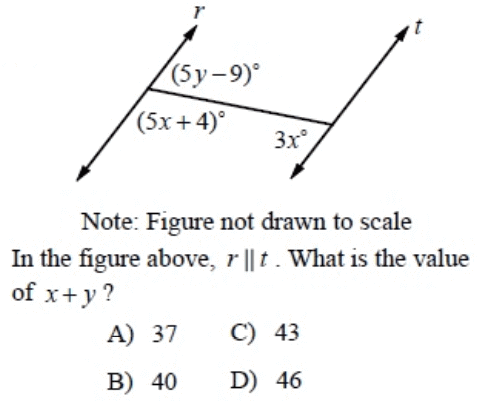
Solution :

Since r || t, 5y - 9 and 3x are alternate interior angle.

5y - 9 = 3x

3x - 5y = -9 ----(1)

5y - 9 and 5x + 4 are linear pair.

5x + 4 + 5y - 9 = 180

5x + 5y - 5 = 180

5x + 5y = 185

x + y = 37  ----(2)

(1) + 5(2) :

3x - 5y + 5(x + y) = -9 + 185

3x - 5y + 5x + 5y = 176

8x = 176

x = 176/8

x = 22

Problem 3 :

Solution :

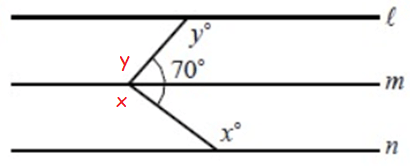
Since n and m are parallel, alternate interior angles are equal.

Since l and m are parallel, alternate interior angles are equal.

x + y + 70 = 360

x + y = 360 - 70

x + y = 290

Problem 4 :

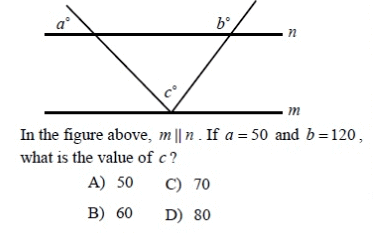
Solution :

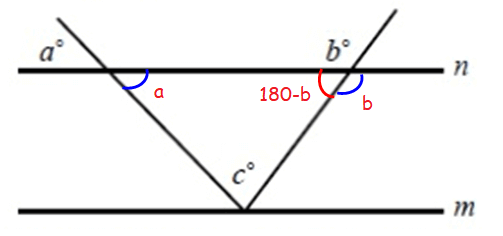
In a triangle, sum of interior angles of triangle is 180°.

a + c + 180 - b = 180

50 + c + 180 - 120 = 180

230 - 120 + c = 180

110 + c = 180

c = 180 - 110

c = 70

Problem 5 :

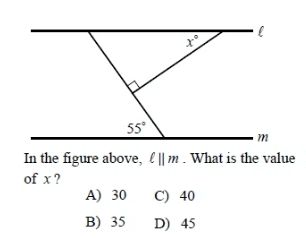
Solution :

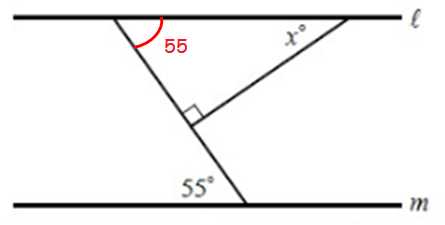
Since l and m are parallel, alternate interior angles are equal.

In a triangle, sum of interior angles of triangle is 180°.

55 + 90 + x = 180

145 + x = 180

x = 180 - 145

x = 35

Problem 6 :

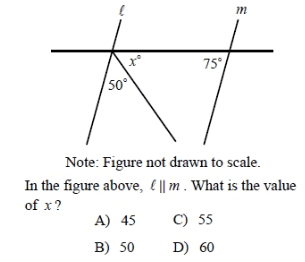
Solution :

Since lines l and m are parallel, corresponding angles will be equal.

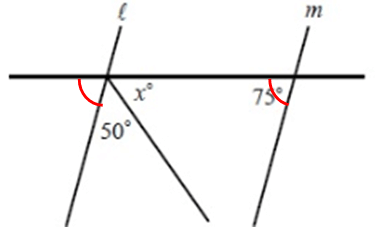
In the line l,

75 + 50 + x = 180

125 + x = 180

x = 180 - 125

x = 55

Problem 7 :

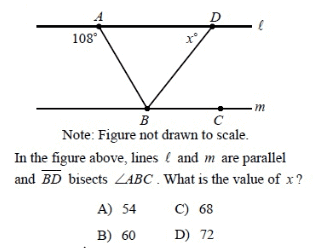
Solution :

108° + ∠BAD = 180°

∠BAD = 180° - 108°

∠BAD = 72°

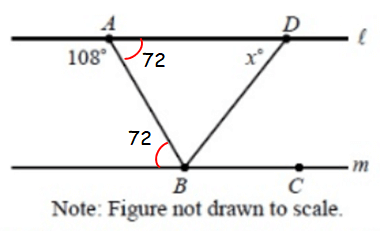
∠ABC = 180° - 72°

∠ABC = 108°

∠ABC = ∠ABD + ∠DBC

Since ∠ABD = ∠DBC,

∠ABC = ∠ABD + ∠ABD

∠ABC = 2∠ABD

108° = 2∠ABD

Divide both sides by 2.

54° = ∠ABD

In triangle ABD,

72° + 54° + x° = 180°

x + 126 = 180

x = 54

Problem 8 :

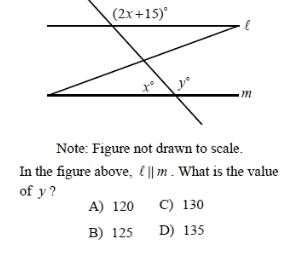
Solution :

x + y = 180 ----(1)

Corresponding angles are equal,

2x + 15 = y

2x-y = -15 ----(2)

(1) + (2) :

x + 2x = 180 - 15

3x = 165

x = 55

Substitute x = 55 in (1).

55 + y = 180

y = 180 - 55

y = 125

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.