MATH OLYMPIAD WORKSHEET FOR GRADE 6

Question 1 :

Peter is now 24p years old. He is thrice as old as John. Find their total age 4 years ago ?

(A)  23p - 4  (B)  32p - 8  (C)  8p - 32  (D)  4p - 32

Solution :

Present age of Peter  =  24 p

Age of peter  =  3 (John's age)

Age of Peter  =  24p  =  3(8p)

Present age of John  =  8p

Four years ago :

Age of Peter  =  24p - 4

Age of John  =  8p - 4

Total age  =  24p - 4 + 8p - 4

  =  32p - 8

Question 2 :

A cap costs n rupee and a belt and 2 caps but is short of $70. How much does he have ?

Express your answer in terms of n rupees.

(A)  3n   (B)  3n + 20  (C)  2n + 70  (D)  n + 70

Solution :

Cost of one cap  =  n rupee

Cost of 1 belt  =  n + 90

Dany wants to buy 1 belt and 2 caps :

Required cost  =  n + 90 + 2n

  =  3n + 90

Question 3 :

A delivery truck delivers goods from Town A to town B. It can travel at 90 km/h when it is empty but only at 60 km/h when it is loaded with goods. Find the distance between two towns if it can cover 6 trips in 12 hours.

(A)  48 km  (B)  36 km  (C)  72 km  (D)  12 km

Solution :

Time  =  Distance / Speed

Time taken to cover 1 trip  =  (D/60) + (D/90)

=  (3D + 2D)/180

=  5D/180

Time taken to cover 6 trips  =  6 ⋅ (5D/180)

12  =  30D/180

12  =  D/6

D  =   12(6)  =  72 km

Hence the distance covered in 6 trips is 72 km.

Question 4 :

500 books are to be distributed unevenly to a certain number of libraries. Each library however, must not get more than 15 books. How many libraries, at least, will get the same number of books ?

(A)  4  (B)  5  (C)  33  (D)  45

Solution :

Let us consider that we distribute the books in the pattern

1, 2, 3, 4, 5, .........,15

Total number of books distributed :

1 + 2 + 3 + ............. + 15 

=  n(n + 1) / 2 

=  15(15 + 1) / 2

=  15 (16) / 2

=  120

We may distribute 120 books for 15 libraries by distributing 1 book for 1st library, 2 books for 2nd library and so on.

120 books  --->  15 libraries

(Each library is getting different number of books)

240 books  ----> 30 libraries 

(Two libraries are getting same number of books)

360 books  ----> 45 libraries 

(Three libraries are getting same number of books)

480 books  ----> 60 libraries 

(Four libraries are getting same number of books)

Number of books distributed so far  =  480

Remaining number of books  =  500 - 480  =  20

By distributing these 20 books, we might have 1 library  will get the same number of books as we have in the above 4 libraries.

Hence the answer is (4 + 1)  =  5.

Question 5 :

Last year, the ratio of the number of girls to the number of boys in the table tennis CCA was 4 : 7. This year, 18 girls joined the club and the number of girls joined the club and the number of girls and boys become the same. How many pupils were in the club this year ?

(A)  84  (B)  42  (C)  74  (E)  75

Solution :

Ratio of the number of girls to the number of boys 

=  4 : 7

Number of girls  =  4x

Number of boys  =  7x

Number of girls joined this year  =  18

Total number of girls in this year  =  4x + 18

4x + 18  =  7x

7x - 4x  =  18

3x  =  18

x  =  6

Number of pupils  =  7x + 4x + 18

  =  11x + 18

  =  11(6) + 18

  =  84

Hence the total number of pupils is 84.

Question 6 :

The model of a bus is made using a scale  of 1:20. This means that 20 cm of the actual bus is represented by 1 cm of the model. If the length of actual bus is 12 m, calculate the length of the model. Express your answer in centimeters.

(A)  40 cm (B)  60 cm  (C)  50 cm (E)  70 cm

Solution :

The ratio of lengths of actual bus to the modal bus is 1:20.

Length of actual bus  =  1x

Length of modal bus  =  20x

20x  =  12 m

x   =  12/20  =  0.6 m

But we have to represent the answer in cm.

So, 0.6 x 100  =  60 cm.

Hence the length of the modal bus is 60 cm.

Question 7 :

Express 50 minutes  as the ratio of 2 hours 5 minutes.

(a)  2 : 3 (B)  4 : 5 (C)  2 : 5  (E)  3 : 5

Solution :

If two quantities are in same kind, we may compare them using ratio.

50 minutes

2 hours  =  2 (60 minutes)

  =  120 minutes

2 hours 5 minutes  =  120 + 5  ==>  125 minutes

  =  50 : 125

=  2 : 5

Question 8 :

The figure shown below 3 identical rectangles A, B and C and 2 areas shaded in black are the same size.

Given that 2/5 of rectangle A is shaded in black, what is the ratio of the shaded areas to the area of the whole figure ?

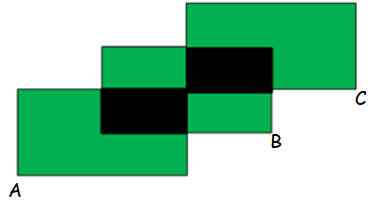
(A)  2/15  (B)  4/15  (C)  4/7  (D)  4/11

Solution :

Given that :

  =  2/5 of rectangle 

By writing it as ratio we get 2 : 5, which represents the ratio of shaded area in black to the given rectangle.

Let x be the shaded area in black and y be the area of the rectangle.

x/y  =  2/5

x  =  (2/5)y

Shaded area in black  =  x + x  =  2x

Area of rectangle A  =  y

Area of rectangle C  =  y

Area of rectangle B  =  y - 2x

  =  y - 2(2y/5)

  =  y - (4y/5)

  =  y/5

Shaded area in black : Area of rectangle

  =  2x / [(y + y + (y/5)]

=  2(2y/5) / [11y/5]

=  (4y/5) / (11y/5)

=  4 : 11

Hence the answer is 4/11.

Question 9 :

There were 4960 people at the carnival. The ratio of the number of men to the number of women was 5 : 6, while the ratio of the number of women to the number of children was 2 : 3.

Some people joined the carnival and some people left. After that there were 5208 people at the carnival. The ratio of the number of men to the number women to the number of children then becomes 1 : 2 : 5. What was the increase in the number of children ?

(A)  1023  (B)  845  (C)  948  (D)  1100

Solution :

Total number of people in the carnival  =  4960

Let A, B and C be the ratio of men, women and children respectively.

A : B  =  5 : 6 and B : C  =  2 : 3

In order to make 2 as 6, we have to multiply the entire ratio by 3. So, we get

B : C  =  6 : 9

A : B : C  =  5 : 6 : 9

5k + 6k + 9k  =  4960

20k  =  4960

k  =  4960/20  =  248

At first, the number of children in the carnival 

  =  9(248)  ==>  2232

After some people joined and some people left,

The total number of people at present in the carnival 

=  5208

1x + 2x + 5x  =  5208

8x  =  5208

x  =  5208/8  ==>  651

At present, the number of children (5x)  =  5(651)  

  =  3255

Increased number of children  =  3255 - 2232

=  1023

Question 10 :

The ratio of the number of marbles in box A to the number of marbles in box B is 3 : 5.

If 1/3 of the marbles in Box A are transferred to Box B and then 1/3 of the marbles in Box B is transferred to Box A, what will be the ratio of the number of marbles in Box A to the number of marbles in Box B ?

(A)  2 : 1  (B)  1 : 1  (C)  1 : 3  (D)  2 : 3

Solution :

Number of marbles in Box A  =  3x

Number of marbles in Box B  =  5x

After the 1^st transformation :

1/3 of number of marbles is going to be transferred from Box A to Box B.

Number of marbles in Box A  =  3x - (1/3) of 3x

  =  3x - x

  =  2x

Number of marbles in Box B  =  5x + (1/3) of 3x

  =  5x + x

  =  6x

After the second transformation :

1/3 of number of marbles is going to be transferred from Box B to Box A.

Number of marbles in Box B  =  6x - (1/3) of 6x

  =  6x - 2x

  =  4x

Number of marbles in Box A  =  2x + (1/3) of 6x

  =  2x + 2x

  =  4x

The ratio of number of marbles in Box A to the number of marbles in Box B.

  =  4x : 4x 

  =  1 : 1

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.