MATH PRACTICE PROBLEMS FOR GRADE 7 WITH ANSWERS

Question 1 :

The sum of the digits of a two digit number is 15 and if 9 is added to the number the digits are interchanged.Find the required number. 

(A) 78               (B) 19           (C) 82

Solution :

Let "xy" be the required two digit number

x + y  =  15  ------(1)

xy + 9  =  yx

10x + 1y + 9  =  10y + 1x

10x - x + 1y - 10y  =  -9

9x - 9y  =  -9  ------(2)

Divide (2) by 9, we get

x - y  =  -1 ------(2)

                  x + y  =  15

                 x - y  =  -1

               ------------------

                2x  =  14  ==> x  =  7

By applying the value of x in the first equation, we get

7 + y  =  15

Subtract both sides by 7, 

y  =  15 - 7  =  8

So, the required number is 78.

Question 2 :

Two trains with a speed of 35 km per hour and 28 km per hour respectively,starting at the same time, run in the opposite directions between two stations A and B, 315 km apart.Find where they will meet

(A) 180 km apart from A     (B) 130 km apart from A

(C) 175 km apart from A

Solution :

Let both trains meet at x distance from station A

the time when they meet will be equal

x/35  =  (315-x)/28

x/5  =  (315-x)/4

4x  =  1575 - 5x

9x  =  1575  ==> x  =  175

t  =  x/35  ==>  175/35 ==> 5

So, the trains will meet at 175 km apart from station A and after 5 hrs.

Question 3 :

The sum of two number is 135 and are in the ratio 4:5.Find the required numbers. 

(A) 80,95      (B) 60,75        (C) 30,35

Solution :

Let the two numbers be 4x and 5x

4x + 5x  =  135

9x  =  135

x  =  135/9  ==>  15

4x  =  4(15)  =  60

5x  =   5(15)  =  75

So, the required numbers are 60 and 75.

Question 4 :

The sum of two numbers is 3000. If 8% of one number is equal to 12% of the other, find the numbers.

(A) 1800 and 1200        (B) 2240 and 2800 

(C) 2700 and 3100

Solution :

Let the two numbers be x and y.

Given, x + y = 3000

Also, 

We got x = 3y/2

But x + y = 3000

3y/2 + y = 3000

5y/2 = 3000

y = 3000 × 2 / 5 = 1200

So, x = 3(1200)/2 = 1800

Hence the numbers are 1800 and 1200

Question 5 :

Solve the following 2(6x-5)  =  (3x+2) + 6

(A) 2               (B) 5                (C) 3

Solution :

2(6x-5) = (3x+2) + 6

12x - 10 = 3x + 2 + 6

12x - 3x  =  8 + 10

9x  =  18

Divide both sides by 9

x  =  18/9  =  2

Question 6 : 

A chord of length 16 cm is drawn in a circle of radius 10 cm. Find the distance of the chord from the centre of the circle.

(A) 30 cm          (B) 25 cm        (C) 12 cm

Solution :

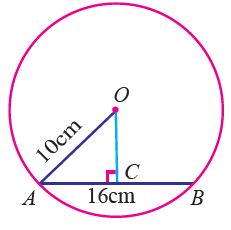
AB is a chord of length 16 cm

C is the midpoint of AB.

OA is the radius of length 10 cm

AB = 16 cm

AC = (1/2) ⋅ 16 = 8 cm

OA = 10 cm

In a right triangle OAC.

OC² = OA² - AC²

OC²  = 10² - 8²

OC²  = 100 - 64 = 36 cm

OC = 6 cm

So, the distance of the chord from the centre is 6 cm.

Question 7 :

In the figure, O is the center of the circle, <ABO  =  30°, where A, B and C are points on the circle . What is the value of "x" ?

(A)  60°            (B)  100°             (C)  50°

Solution :

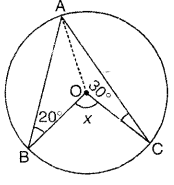
In triangle OAB, we have 

OA  =  OB

<OAB  =  <OBA  =  20°

In triangle OAB, we have 

OA  =  OC

<OAC  =  <OCA  =  30°

<BAC  =  <OAB + <OAC

    =  20° + 30°  =  50°

x  = <BOC  =  2<BAC

  =  2(50°)  =  100°

So, the required angle is 100°.

Question 8 :

The base of the parallelogram is twice the height.If the area is 578 find the base and height.

(A) Height = 10 cm and Base = 20 cm

(B) Height = 17cm and Base = 34 cm

(C) Height = 15 cm and Base = 10 cm

Solution :

Let "x" be the base of the parallelogram

height  =  2x

Area of parallelogram  =  578

x (2x)  =  578

2x²  =  578  ==> x²  =  289

x  =  17 cm

2x  =  2(17)  =  34 cm

So, the base and height of the parallelogram are 17 and 34 cm respectively.

Question 9 :

The perimeter of a triangle field is 144 m and the ratio of the sides is 3:4:5.Find the area of the field.

(A) 318 m²           (B) 522 m²          (C) 864 m ²

Solution :

Sides of the triangle are 3x, 4x and 5x

Perimeter of the triangle  =  144 m

3x + 4x + 5x  =  144

12x  =  144

Divide both sides by 12

x  =  144/12  =  12

3x  =  3(12)  =  36

4x  =  4(12)  =  48

5x  =  5(12)  =  60

Area of scalene triangle  =  √s (s-a) (s-b) (s-c)

s  =  144/2  =  72

s - a = 72 - 36  =  36

s - b = 72 - 48  =  24

s - c = 72 - 60  =  12

=  √(72 ⋅ 36 ⋅ 24 ⋅ 12)

   =  864 m²

Question 10 :

The circumference of a circle exceeds the diameter by 20 cm. Find the radius of the circle. 

Solution :

Let the radius of circle of  =  r m. 

Then circumference  =  2 πr 

Since, circumference exceeds diameter by 20 

2 πr  =  d + 20 

 2 πr  =  2r + 20 

 2 × (22/7) × r  =  2r + 20

 44r/7 - 2r  =  20

 (44r - 14r)/7  =  20

 30r/7  =  20 

 r  =  (7 ⋅ 20)/30

 r  =  14/3

So, the radius of circle is 14/3 cm.

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.