MATH PRACTICE TEST FOR 8TH GRADE ONLINE

Question 1 :

Find the maximum value of quadratic function

n ²  - 6n - 55 

(A) -64               (B) 55              (C) -48

Solution :

We have a formula to find the maximum value  of a quadratic equation.

x-coordinate of maximum value  =  -b/2a

a  =  1, b  =  -6 and c  =  -55

-b/2a  =  - (-6)/2(1)

  =  6/2

  =  3

Maximum value  =  f(3)

  =  (3)² - 6(3) - 55

  =  9 - 18 - 55

 =  9 - 73

  =  -64

Hence the maximum value is -64.

Question 2 :

Find a rational number between 3/4 and 4/5

(A) 21/40          (B) 31/40        (C) 41/40

Solution :

Let a =  3/4 and b = 4/5

Formula to find rational number between two rational numbers

  =  (1/2)(a + b)

  =  (1/2) (3/4 + 4/5)

L.C.M of 4 and 5 is 20.

  =  (1/2) (15/20 + 16/20)

  =  (1/2) [(15 + 16)/20]

  =  (1/2) (31/20)

  =  31/40

Hence the required rational number between the given rational numbers is 31/40.

Question 3 :

Simplify (1 - (1/2)) + (3/4 - 1/4)

(A) 1          (B) 0        (C)  2

Solution :

  =  (1 - (1/2)) + (3/4 - 1/4)

  =  (2-1)/2 + [(3 - 1)/4]

  =  1/2 + [(3 - 1)/4]

  =  (1/2) + (2/4)

  =  (2 + 2)/4

  =  1

Hence the answer is 1.

Question 4 :

Cube root of 125/256

(A) 5/4          (B) 25/4          (C) 5/6

Solution :

∛(125/256) 

To find cube root of the given fraction, we have to decompose both numerator and denominators into prime factors.

  =  ∛(5⋅ 5 ⋅ 5) / (2 ⋅ 2 ⋅ 2 ⋅ 3 ⋅ 3 ⋅ 3)

We may group them as triples.

  =  5/6

Question 5 :

Find the smallest number by which 81 must be divided to obtain a perfect cube.

(A) 2          (B) 3          (C) 4

Solution : To find the number required to divide 81 such that the quotient is a perfect cube, we have to decompose 81 into prime factors.    =  ∛81   =  ∛(3⋅3⋅3⋅3) When we group the prime factors inside the cube root as triples, we left over with 3. That is 3.   So, 3 is the smallest number required to divide 81 so that the quotient is a perfect cube.

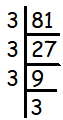Question 6 :

Find the fifth term of the sequence whose second term is 8 and third term is 14.

Solution :

Second term  =  8

Third term  =  14

General term of the arithmetic sequence :

a _n  =  a + (n - 1) d

Second term (a + d)  =  8  ---(1)

Third term (a + 2d)  =  14 ----(2)

(1) - (2)

a + d - (a + 2d)  =  8 - 14

-d  =  -6

d  =  6

By applying the value of d in (1), we get the value of a

a + 6  =  8

a  =  8 - 6

a  =  2

Fifth term  =  a + 4d

  =  2 + 4(6)

  =  2 + 24

  =  26

So, the fifth term is 26.

Question 7 :

Find AC when AB  =  15 cm, AD  =  10 cm, AE  =  8 cm

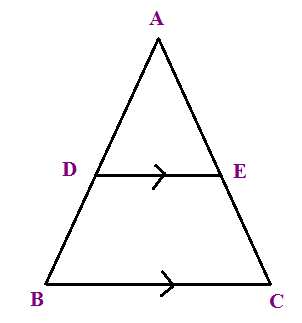
(A)  12 cm       (B)  10 cm        (C)   13 cm

Solution :

AB = AD + DB

15 = 10 + DB

DB = 15 - 10

DB = 5

10/5  =  8/EC

EC  =  8/2  =  4

AC  =  AE + EC

AC  =  8 + 4  =  12

So, length of AC is 12 cm.

Question 8 :

Angle ABC measures 250°, find the measure of minor of arc AC.

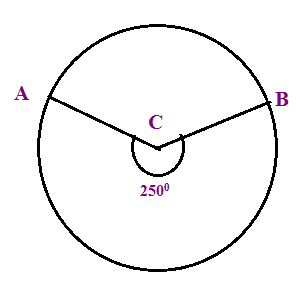
(A)  150°          (B)  110°         (C)  140°

Solution :

Measure of minor arc  =  360 - 250

=  110°

Question 9 :

Find the mean of all odd numbers between 80 and 88.

(A) 84            (B) 30             (C) 62

Solution :

Odd numbers between 80 and 88 are

81, 83, 85, 87

Mean of above numbers  =  (81 + 83 + 85 + 87) / 4

=  336/4

=  84

Question 10 :

The number of times a particular observation occur in a data is called its __________

(A) Frequency          (B) Mean         (C) Median

Solution :

The number of times a particular observation occur in a data is called its frequency.

Answers

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.