MATH PROBLEMS

Problem 1 : 

A clown's face consists of an isosceles triangle PQR on top of a sector of a circle as shown below.  

The diameter of the circle is 20 centimeters. 

The base of the triangle is 16 centimeters and its sloping sides are 17 centimeters long. 

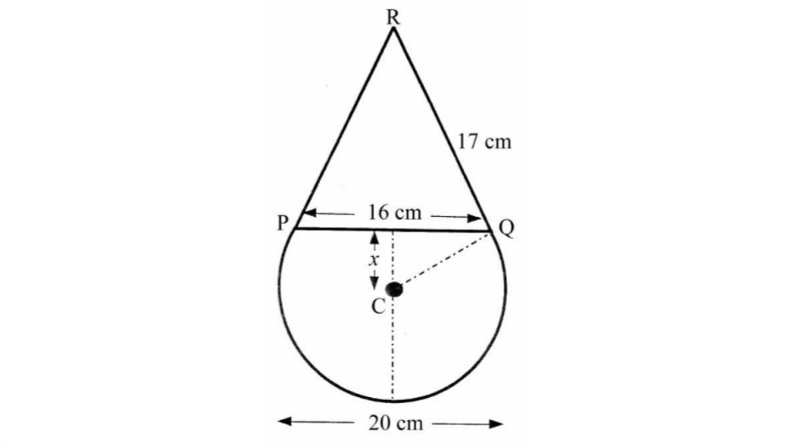
a) Calculate x, the distance in centimeters from the center of the circle to the base of the triangle. 

b)  Calculate the total height of the figure. 

Solution : 

In the diagram shown above, clearly the radius is 10 centimeters. 

It is illustrated in the diagram shown below. 

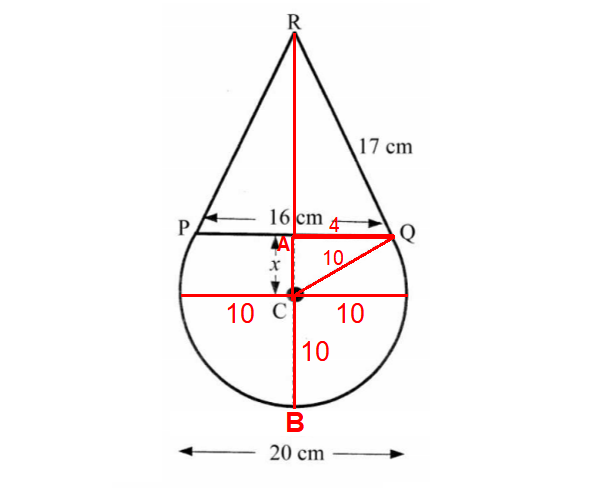
Calculating the value of x : 

In the right triangle CAQ, by Pythagorean theorem, we have

CA² + AQ²  =  CQ²

x² + 4²  =  10²

x² + 16  =  100

Subtract 16 from each side.

x²  =  84

Take radical on each side.

x  ≈  9.17

Finding the length of RA :

In the right triangle RAQ, by Pythagorean theorem, we have

RA² + AQ²  =  RQ²

RA² + 4²  =  17²

RA² + 16  =  289

Subtract 16 from each side.

RA²  =  273

Take radical on each side.

RA  ≈  16.52

Calculating the total height of the figure :

In the last diagram above, the total height of the figure is RB. 

RB  =  RA + AC + CB

RB  ≈  16.52 + 9.17 + 10

RB  ≈  35.69

Hence, the total height of the figure is about 35.69 centimeters. 

Problem 2 : 

There is a right triangle ABC where ∠B  =  90°, AB  =  6 and BC  =  8. A line segment is drawn from B so that it is perpendicular to side AC at point D. What is the length of this line segment ?

Solution : 

Start with sketching the graph. 

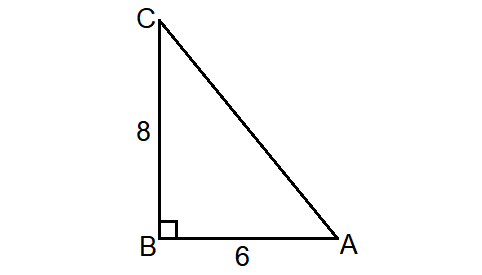
In the right triangle ABC shown above, by Pythagorean theorem, we have 

AC²   =  BA² + BC²

AC²   =  6² + 8²

AC²   =  36 + 64

AC²   =  100

Take radical on each side. 

AC  =  10

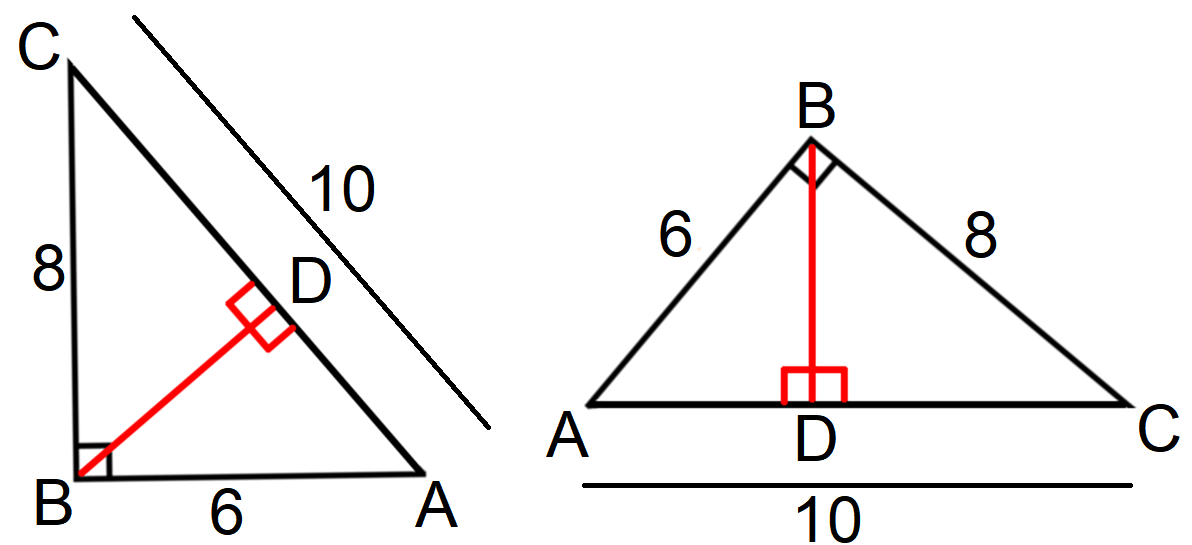
Let us find the area of the triangle ABC by taking AB as base and BC as height. 

Area of triangle ABC  =  1/2 ⋅ AB ⋅ BC

Area of triangle ABC  =  1/2 ⋅ 6 ⋅ 8

Area of triangle ABC  =  24 square units

Area of the triangle ABC by taking AC as base and BD as height.

Area of triangle ABC  =  24 square units

1/2 ⋅ AC ⋅ BD  =  24

Substitute AC  =  10.

1/2 ⋅ 10 ⋅ BD  =  24

Simplify. 

5 ⋅ BD  =  24

Divide each side by 5. 

BD  =  24 / 5

BD  =  4.8

Hence, the length of the perpendicular from B to AC is 4.8 units. 

Problem 3 : 

A manufacturing company finds that they can sell 300 items if the price per item is $2.00, and 400 items if the price is $1.50 per item. If the relationship between the number of items sold x and the price per item p is a linear one, find a formula that gives x in terms of p.

Solution : 

From the given information, we can get two points in the form (x, p). 

They are : 

(300, 2) and (400, 1.5)

Because we know the two points of the given linear relationship, easily we can get the formula (linear equation) that gives x in terms of p using two points form equation of a straight line.  

The formula to find equation of a straight line when we know two points : 

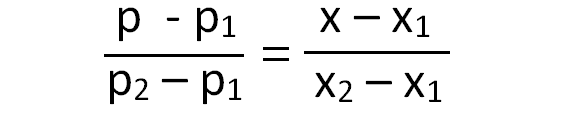
Substitute :

(x₁ - p₁)  =  (300, 2)

(x₂, p₂)  =  (400, 1.5)

Then, we have

(p - 2) / (1.5 - 2)  =  (x - 300) / (400 - 300)

(p - 2) / (- 0.5)  =  (x - 300) / 100

(p - 2) / (- 1/2)  =  (x - 300) / 100

(p - 2) ⋅ (- 2/1)  =  (x - 300) / 100

- 2(p - 2)  =  (x - 300) / 100

Multiply each side by 100.

- 200(p - 2)  =  x - 300

- 200p + 400  =  x - 300

Add 300 to each side.

- 200p + 700  =  x

Hence, the formula that gives x in terms of p is 

x  =  - 200p + 700 

Justification : 

When p  =  2, 

x  =  - 200(2) + 700

x  =  - 400 + 700

x  =  300

When p  =  1.5, 

x  =  - 200(1.5) + 700

x  =  - 300 + 700

x  =  400

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.