MATHEMATICAL INDUCTION PROBLEMS WITH SOLUTIONS

The process of induction involves the following steps.

Mathematical Induction Problems With Solutions

Question 1 :

By the principle of mathematical induction, prove that, for n ≥ 1

1³ + 2³ + 3³ + · · · + n³ = [n(n + 1)/2]²

Solution :

Let p(n) =  1³ + 2³ + 3³ + · · · + n³ = [n(n + 1)/2]²

Step 1 :

put n = 1

p(1)  = 1³ + 2³ + 3³ + · · · + 1³ = [1(1 + 1)/2]²

  1  =  1

Hence p(1) is true.

Step 2 :

Let us assume that the statement is true for n = k

p(k)  =  1³ + 2³ + 3³ + · · · + k³ = [k(k + 1)/2]²   -----(1)

We need to show that P(k + 1) is true. Consider,

Step 3 :

Let us assume that the statement is true for n = k + 1

p(k + 1)  =  1³ + 2³ + 3³ + · · · + (k + 1)³ = [(k + 1)(k + 2)/2]²

 1³ + 2³ + 3³ + · · ·k³ + (k + 1)³ = [(k + 1)(k + 2)/2]²

By applying (1) in this step, we get

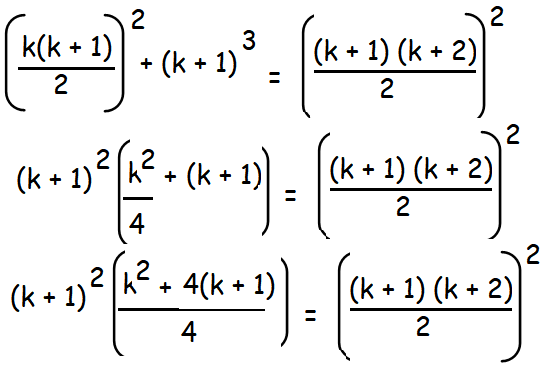
(k + 1)² (k² + 4k + 4)/4  =  [(k + 1)(k + 2)/2]²

(k + 1)² (k + 2)² /4  =  [(k + 1)(k + 2)/2]²

By taking square for the entire terms, we get

  [(k + 1)(k + 2)/2]²  =   [(k + 1)(k + 2)/2]²

Hence, by the principle of mathematical induction, for n≥1 

1³ + 2³ + 3³ + · · · + n³ = [n(n + 1)/2]²

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.