MATHEMATICAL INDUCTION QUESTIONS

Question 1 :

Using the Mathematical induction, show that for any natural number n,

1/(2.5) + 1/(5.8) + 1/(8.11) + · · · + 1/(3n − 1)(3n + 2) = n/(6n + 4)

Solution :

Let p(n) =  1/(2.5) + 1/(5.8) + 1/(8.11) + · · · + 1/(3n − 1)(3n + 2) = n/(6n + 4)

Step 1 :

put n = 1

p(1)  =  p(n) =  [1/(3 − 1)(3 + 2) = 1/(6 + 4)

  1/2(5)  =  1/10

1/10  =  1/10

Hence p(1) is true.

Step 2 :

Let us assume that the statement is true for n = k

  1/(2.5) + 1/(5.8) + 1/(8.11) + · · · + 1/(3K − 1)(3K + 2) = K/(6K + 4)

We need to show that P(k + 1) is true. Consider,

Step 3 :

Let us assume that the statement is true for n = k + 1

p(k+1) 

  1/(2.5) + 1/(5.8) + 1/(8.11) + · · · + 1/(3K + 2)(3K + 5) = (K+1)/(6K+10)

By applying (1) in this step, we get

L.H.S

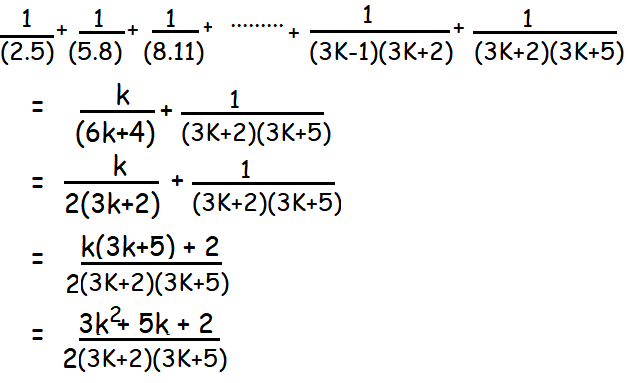
  =  (k+1)(3k+2) / 2(3k+2) (3k+5)

  =  (k+1)/(6k+10)  ----->R.H.S

 for any natural number n,

1/(2.5) + 1/(5.8) + 1/(8.11) + · · · + 1/(3n − 1)(3n + 2) = n/(6n + 4)

Question 2 :

Prove by Mathematical Induction that

1! + (2 × 2!) + (3 × 3!) + ... + (n × n!) = (n + 1)! − 1.

Solution :

Let p(n)  =  1(1!) + 2(2!) + 3(3!) + ... + n(n!) = (n+1)! - 1

Step 1 :

Put n = 1,

p(n)  =  1(1!) + 2(2!) + 3(3!) + ... + n(n!)

Then, LHS = 1(1!) = 1 ⋅ 1 = 1

And   RHS = (1 + 1)! - 1   = 2! - 1 = 2 - 1 = 1

So, both LHS and RHS = 1 and equation is true at n = 1.

Hence p(1)  is true.

Step 2 :

put n = k,

The equation is assumed to be true, and is 

1(1!) + 2(2!) + 3(3!) + ...... + k(k!) = (k+1)! - 1  ------------ (1)

We need to show that P(k + 1) is true. Consider,

Step 3 :

Let us assume that the statement is true for n = k + 1

put n = k + 1,

1(1!) + 2(2!) + 3(3!) + ...... + k(k!) + (k+1)[(k+1)!] = [(k+1)+1]! - 1

{1(1!) + 2(2!) + 3(3!) + ...... + k(k!)} + (k+1)[(k+1)!]  = (k+2)! - 1

{ (k+1)! - 1 } + (k+1)[(k+1)!]  = (k+2)! - 1

(k+1)!  +  (k+1)[(k+1)!]  -  1    =  (k+2)! - 1

 (k+1)! [ 1 + (k+1) ]  -  1  =  (k+2)! - 1

 (k+1)!  x  (k+2) - 1  =  (k+2)! - 1

(k+2)! - 1   =  (k+2)! - 1

Hence it is proved.

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.