MATH OLYMPIAD ONLINE QUIZ

Question 1 :

Find the value of 

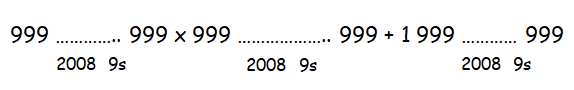
Solution :

To understand this problem, let us take an example problem.

99 x 99 + 199

  =  99 x 99 + (100 + 99) 

  =  99 x (100 - 1) + (100 + 99)

Using distributive property, we may distribute 99.

  =  9900 - 99 + 100 + 99

  =  10000

By applying the same concept in the given problem, we get

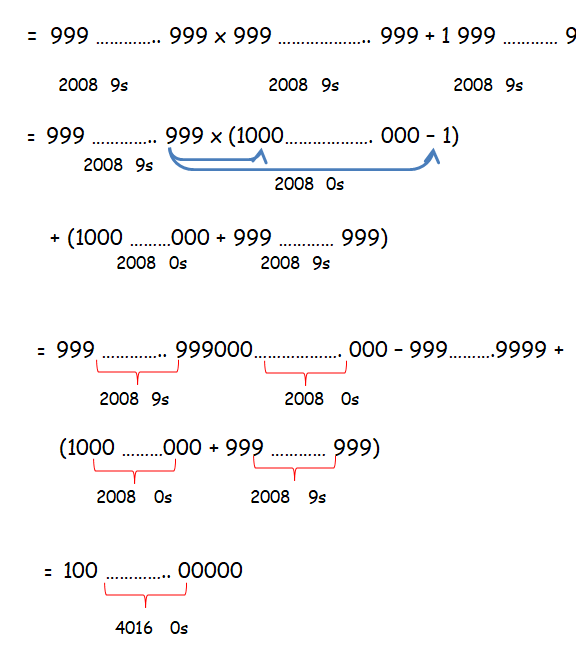
Question 2 :

On 1^st March some years ago, one US Dollar could be exchanges for 1.45 Singapore dollar. On the same day, 1000 Thai Bhat could buy 50 Singapore dollars. How much US dollars could 29000 Thai Bhat buy on that day ?

(A)  500  (B)  2000  (C)  1000   (D)  1500

Solution :

One US Dollar  =  1.45 Singapore Dollar

1000 Thai Bhat  =  50 Singapore Dollars

1.45 Singapore dollar  =  1 US dolar

1 Singapore dollar  =  (1/1.45) US dollar  ----(1)

1 Singapore dollar  =  (1000/50) Thai Bhat

1 Singapore dollar  =  20 Thai Bhat ----(2)

(1)  =  (2)

20 Thai Bhat  =  1/1.45 US dollar

1 Thai Bhat  =  (1/29) US dollar

29000 Thai Bhat  =  (29000/29) US dollar

29000 Thai Bhat  =  1000 US dollars

Question 3 :

The average age of seven numbers is 49 y, if 1 is added to the first number, 2 is added to the second number, 3 is added to the third number and so on upto the seventh number, what is the new average ?

(A)  53y  (B)  53y + 1  (C)  49y + 4  (D)  7y + 13

Solution :

Average of seven numbers  =  49y

Sum of seven numbers / 7  =  49y

Sum of seven numbers  =  49y (7)  =  343 y

Sum of values going to be added  =  1 + 2 + 3 + ...+ 7

  =  n(n +1)/2

  =  (7 x 8)/2

  =  28

Sum of seven numbers + 28  =  343y + 28

(Sum of seven numbers + 28)/7  =  (343y + 28) / 7

Average of seven numbers after the changes  =  49y + 4

Question 4 :

Ravi and Harish take 1 hour to clean the fish tank together. If Ravi takes m hours to clean the tank on his own, how long will it take Harish to clean the tank alone ?

(A)  1/m hours   (B)  (m - 1)/m hours   (C)  m/(m - 1) hours 

(D)  (m - 1) hours

Solution :

Number of hours taken by Ravi to clean the tank  =  m

Work done by Ravi in 1 hour  =  1/m

Number of hours taken by Ravi and Harish to clean the fish tank  =  1 hour

Work done by Harish in 1 hour  =  1 - (1/m)

  =  (m - 1)/m

Time taken by Harish to clean the tank alone 

=  m/(m - 1) hours

Question 5 :

Meera had to cut some identical circles of radius 2 cm from the rectangular sheet of paper measuring 60 cm by h cm as shown. What is the maximum number of circle she could cut ?

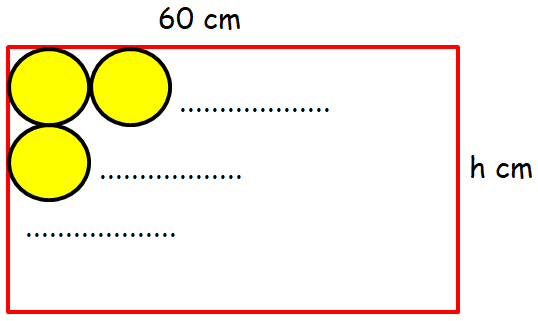
(A)  3.75 h  (B)  3.15 h  (C)  15 h  (D)  12 h

Solution :

Number of circles in one row

  =  Length of rectangle / Diameter of circle

  =  60/4

  =  15

15 identical circles can be placed in one row.

Number of identical circles can be placed in 1 column  =  x

x  =  h / 4

Number of circles in the rectangle  =  15 ⋅ x

  =  15 ⋅ (h/4)

=  3.75 h

Question 6 :

A basket of pears and 2 baskets of oranges weigh 13 kg. 2 baskets of apples and 2 baskets of oranges weigh 22 kg. 3 baskets of pears and 2 baskets of apples weigh 21 kg. How much does each basket of fruit weigh ?

(A)  3, 5, 6  (B)  2, 5, 3  (C)  1, 5, 6  (D)  2, 3, 3

Solution :

Let x, y and z be the cost of 1 basket pears, one basket oranges and 1 basket of apples.

x + 2y  =  13  ----(1)

2y + 2z  =  22  ----(2)

3x + 2z  =  21    ----(3)

(1) + (2) + (3)

4x + 4y + 4z  =  13 + 22 + 21

4(x + y + z)  =  56

x + y + z  =  14 ---(4)

From (2),

y + z  =  11

By applying the value of y + x in (4), we get 

x + 11  =  14

x  =  14 - 11

x  =  3

By applying the value of x in (1), we get

3 + 2y  =  13

2y  =  10

y  =  5

By applying the value of x in (3), we get

3(3) + 2z  =  21

9 + 2z  =  21

2z  =  21 - 9

2z  =  12

z  =  6

Hence the cost of each basket of pears, oranges and apples are 3, 5 and 6 respectively.

Question 7 :

Miss Cussler was born on the 1st January many years ago. In 2002, her age was the sum of all four digits of the year that she was born in. How old was Miss Cussler in 2002 ?

(A)  15 years    (B)  20 years    (C)  22 years   (D)  12 years

Solution :

Form the given information, it is clear that the year of birth of Miss Cussler contains 4 digits.

Let the required year be 1abc.

1abc  =  1000 + 100a + 10b + 1c (Expansion form)

Year of birth  =  Sum of all four digits of the year

2002 - 1abc  =  1 + a + b + c  

2002 - (1000 + 100a + 10b + 1c)  =  1 + a + b + c  

2002 - 1000 - 100a - 10b - c - 1 - a - b - c  =  0

1001 - 101a - 11b - 2c  =  0

1001 - 101a  =  11b + 2c

Let us take a  =  9

11b + 2c  =  1001 - 101(9)

11b + 2c  =  92

11b  =  92 - 2c

b  =  (92 - 2c)/11

So, a  =  9, b = 8 and c = 2.

The required year is 1982.

Required age  =  2002 - 1982  ==> 20 years.

Question 8 :

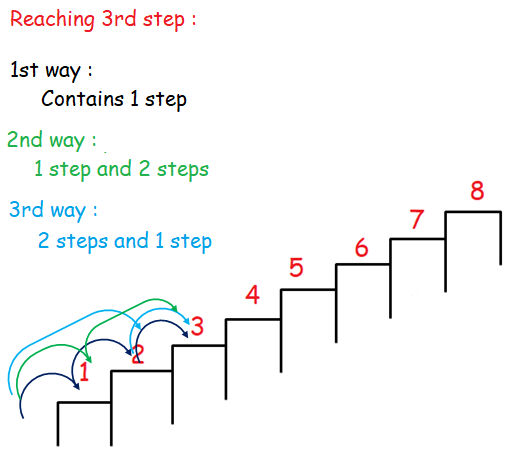
There is a flight of 8 steps in a staircase. A person can either take one or two steps up each time. In how many ways can the person reach the eighth step ?

(A)  64  (B)  56   (C)  21  (D)  48

Solution :

He can reach step 1 in one way.

The diagram given below will describe the number of ways taken by him to reach step 2.

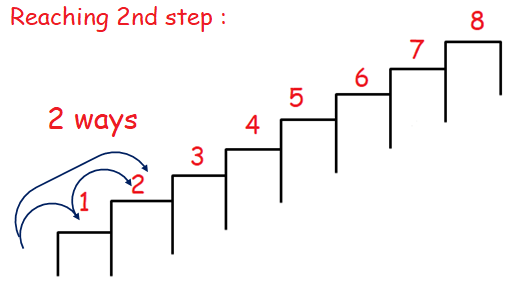
Number of ways to reach step 2 is 2. From the picture given below, number of steps taken by him to reach step 3 is 3 ways.

Number of steps taken to reach step 4 are

Way 1 :

• He can take 1 step (4 times) to reach step 4

Way 2 :

• Going to step 2, then go to step 4.

Way 3 :

• Going to step 1, then go to step 3 (in 2 steps) and reaching step 4 (in one step)

Way 4 :

• Going to step 1 and 2 (contains 1 step each), then go to step 4 (in 2 steps) 

Way 5 :

• Going to step 2 (contains 2 steps), then go to step 3 and 4 (contains 1 step each) 

By writing the above steps as sequence, we get

1, 2, 3, 5, ............

Since this is a fibonacci sequence

Hence in 34 ways a person can reach the 8th step.

Question 9 :

There are ten points on the circumference of a circle. How many triangles can be formed by using any three points as their vertices ?

(A)  720    (B)  10!    (C)  120    (D) 9!

Solution :

There are 10 points on the circumference, it is enough to choose any three points to form a triangle.

Here we use the concept combination, because every arrangements should be unique.

¹⁰ C ₃  =  (10 ⋅ 9 ⋅ 8) / (3 ⋅ 2 ⋅ 1)

  =  10 ⋅ 3 ⋅ 4

  =  120

Hence the answer is 120.

Question 10 :

The figure given below is made up of three-quarter circle and a quadrant. O is the center of the circle. What is the area of the figure ?

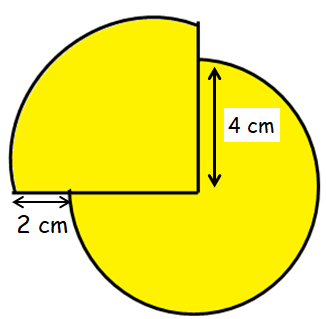
(A)  21 π cm²    (B)  19 π cm²    (C)  14 π cm²  (D)  22 π cm²

Solution :

Area of three-quarter circle  =  (3/4) πr²

Radius of circle  =  4 cm

Radius of quadrant  =  4 + 2  ==>  6 cm

Required area  =  (3/4) πr² + (1/4) πr²

  =  (3/4) π(4)² + (1/4) π(6)²

  =  12 π + 9 π

  =  21 π cm²

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.