MATRIX OPERATIONS PRACTICE

Matrix Operations Practice :

Here we are going to see some practice questions on matrix operations.

Question 1 :

Verify the property A(B + C) = AB + AC, when the matrices A, B, and C are given by

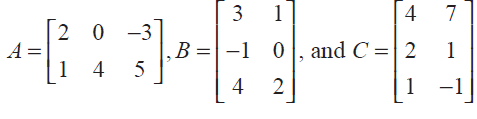
Solution :

In order to verify the given statement A(B + C) = AB + AC, first we have to calculate the terms which is inside the parenthesis.

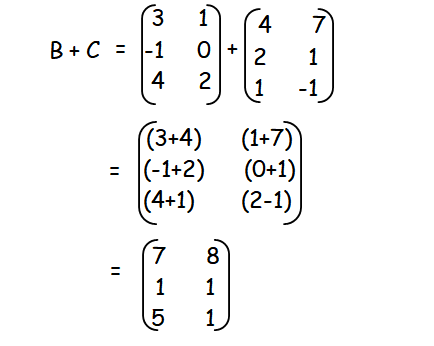
Now we have to find the product of the matrices A and (B + C)

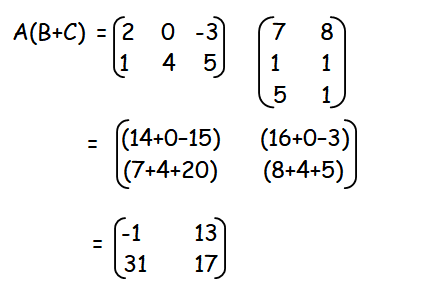
Hence the value of A(B + C) is the matrix given above.

Now let us do calculation in right hand side.

In order to find the value of AB, we have to multiply the matrices A and B.

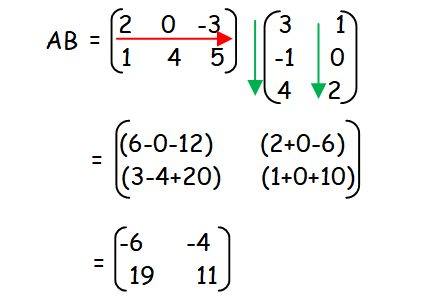
In order to find the value of AC, we have to multiply the matrices A and C.

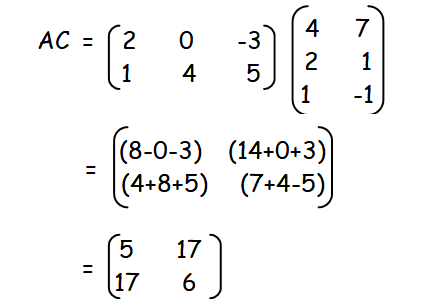
Now we have to add the above matrices AB and AC.

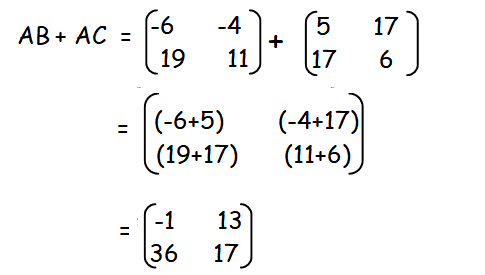
Since we got the same answer for A(B + C) and AB + AC, we may decide that L.H.S  =  R.H.S

Hence it is proved.

Question 2 :

Find the matrix A which satisfies the matrix relation 

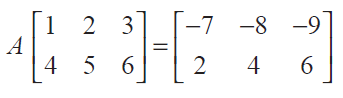
Solution :

By multiplying the matrix A with order m x n by the given matrix with order 2 x 3, we get a matrix with order 2 x 3.

So the required matrix will be in the order 2 x 2.

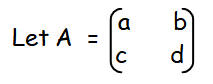
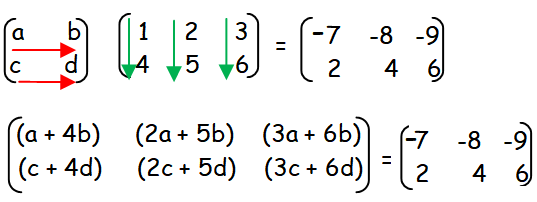
Let us equate the corresponding terms.

a + 4b  =  -7  -------(1) 

2a + 5b  =  -8  -------(2)

c + 4d  =  2  -------(3)

2c + 5d  =  4  -------(4)

By solving the first and second equations, we get the values of a and b respectively.

(1) - (2) 

(2a + 8b) - (2a + 5b)  =  -14 - (-8)

2a + 8b - 2a - 5b  =  -14 + 8

3b  =  -6

b  =  -6/3  ==>  -2

Applying the value of b in first equation, we get

a + 4(-2)  =  -7

a - 8  =  -7

a  =  -7 + 8  ==>  1

By solving the third and fourth equations, we get the values of a and b respectively.

2(3) - (4)

2c + 8d - (2c + 5d)  =  4 - 4

2c + 8d - 2c - 5d  =  0

3d  =  0  ==> d  =  0

Applying the value of b in third equation, we get

c + 4(0)  =  2

c  =  2

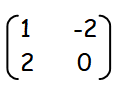
Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.