MEASURES OF CENTER DOT PLOTS

We can find and calculate measures of center and spread from a dot plot.

Example : 

A baseball team manager records the number of runs scored by the team in each game for several weeks. 

1, 3, 1, 7, 2, 0, 11, 2, 2, 3, 1, 3, 4, 2, 2, 4, 5, 2, 6

(i)  Make a dot plot to know how the data is distributed.

(ii)  Find the mean, median, and range of the data.

(iii)  How many runs does the team typically score in a game? Explain.

Solution : 

Answer (i) :

Step 1 : 

Make a real number line.

In the given data, we have values range from from 0 to 11. 

So we have to use a scale from 0 to 11.

Step 2 : 

Draw a dot above the number line for each data value.

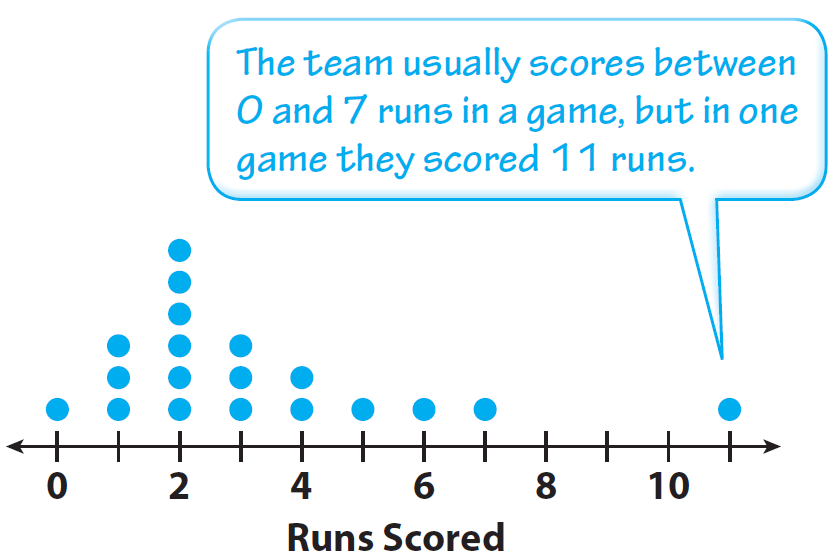
Answer (ii) :

Step 1 : 

To find the mean, find the sum of the data values and divide by the number of data values.

So, the mean is

=  [1(0)+3(1)+6(2)+3(3)+2(4)+1(5)+1(6)+1(7)+1(11)] / 19

=  61 / 19

=  3.21052............

≈  3.2

Hence, the mean is about 3.2.

Step 2 : 

To find the median, count the dots from left to right until you find the middle value. You may need to find the mean of two middle values.

The median is 2.

Step 3 : 

To find the range, read the least and greatest values from the dot plot. Subtract the least value from the greatest.

11 - 0  =  11

The range is 11.

Answer (iii) :

The mean number of runs is 3.2. The median number of runs is 2.

The shape of the dot plot suggests that the out lier 11 may be affecting these measures of center. To see if that is the case, find the mean and median without including the out lier. Compare these values with the original values.

Step 1 : 

Find the mean without including the out lier.

=  [1(0) + 3(1) + 6(2) + 3(3) + 2(4) + 1(5) + 1(6) + 1(7)] / 18

=  50 / 18

=  2.7777............

≈  2.8

Without the out lier, the mean is 2.8, which is less than the original mean of 3.2.

Step 2 : 

Find the median without including the outlier.

Counting from left to right, the median is still 2.

Given that it is not affected by the out lier, the median may be more typical of the data. The team typically scores two runs per game.

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.