MEDIANS AND ALTITUDES OF A TRIANGLE WORKSHEET

Problem 1 :

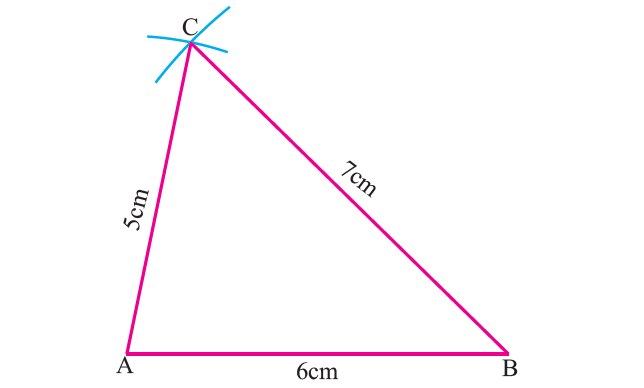
Construct the centroid of ΔABC whose sides are AB = 6cm, BC = 7cm, and AC = 5cm.

Problem 2 :

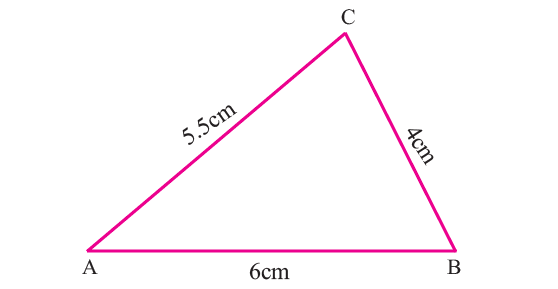
Construct ΔABC whose sides are AB = 6cm, BC = 4cm and AC = 5.5cm and locate its orthocenter.

Problem 3 :

Where is the orthocenter located in each type of triangle ?

(a) Acute triangle

(b) Right triangle

(c) Obtuse triangle

Problem 4 :

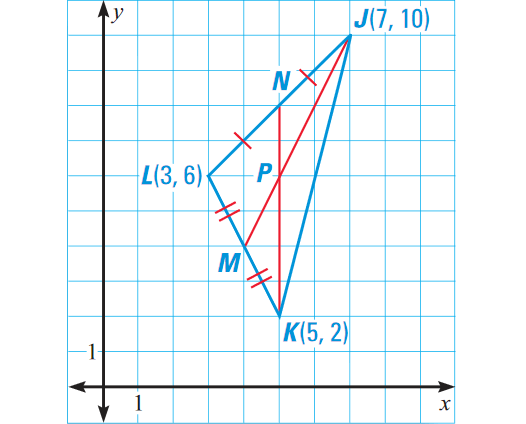
Find the coordinates of the centroid of ΔJKL shown below.

1. Answer :

Step 1 :

Draw ΔABC using the given measurements.

Step 2 :

Construct the perpendicular bisectors of any two sides (AC and BC) to find the mid points D and E of AC and BC respectively.

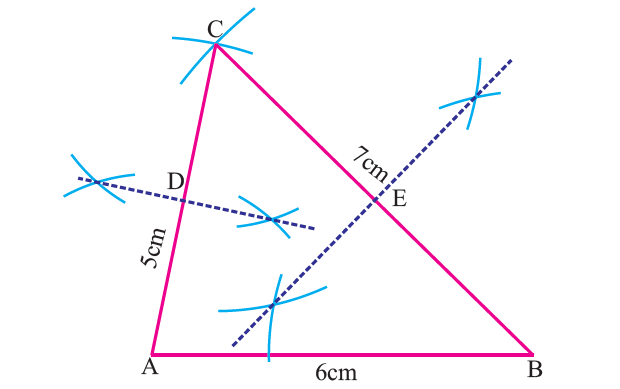
Step 3 :

Draw the medians AE and BD and let them meet at G.

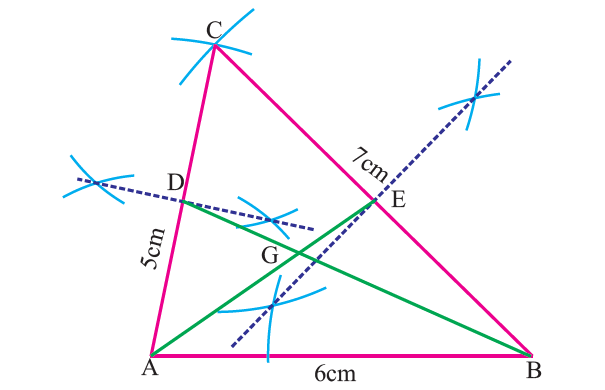
The point G is the centroid of the given ΔABC.

2. Answer :

Step 1 :

Draw ΔABC using the given measurements.

Step 2 :

Construct altitudes from any two vertices (A and C) to their opposite sides (BC and AB respectively).

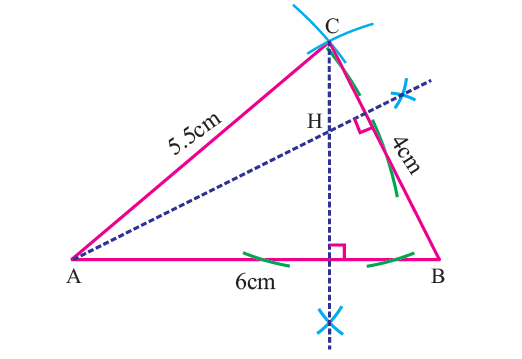
The point of intersection of the altitudes H is the orthocenter of the given ΔABC.

3. Answer :

Draw an example of each type of triangle and locate its orthocenter.

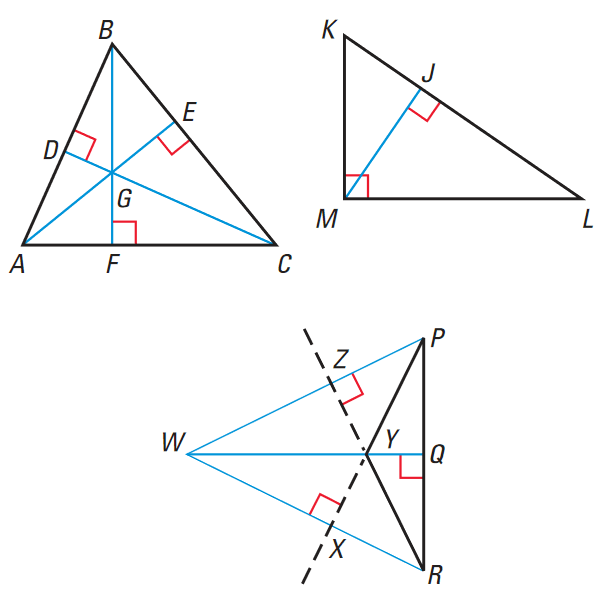
(a) Acute Triangle :

ΔABC is an acute triangle. The three altitudes intersect at G, a point inside the triangle.

(a) Right Triangle :

ΔKLM is a right triangle. The two legs LM and KM, are also altitudes. They intersect at the triangle's right angle. This implies that the orthocenter is on the triangle at M, the vertex of the right angle of the triangle.

(a) Obtuse Triangle :

ΔYPR is an obtuse triangle. The three lines that contain the altitudes intersect at W, a point that is outside the triangle.

4. Answer :

We know that the centroid is two thirds of the distance from each vertex to the midpoint of the opposite side.

Choose the median KN. Find the coordinates of N, the midpoint of JL.

The coordinates of N are

[(3 + 7)/2, (6 + 10)/2] = (10/2, 16/2)

= (5, 8)

Find the distance from vertex K to midpoint N. The distance from K(5, 2) to N(5, 8) is 8 - 2, or 6 units.

Determine the coordinates of the centroid, which is 2/3⋅6 or 4 units up from vertex K along the median KN.

So, the coordinates of centroid P are

(5, 2 + 4) or (5, 6)

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.