METHODS OF PRIME FACTORIZATION

Expressing a given number as a product of factors that are all prime numbers is called the prime factorization of a number.

To find the prime factors of  a composite number, we do the prime factorization by the following methods.

1. Division Method

2. Factor Tree Method 

Division Method

Using Division Method, we can find the prime factorization of 36 as follows :

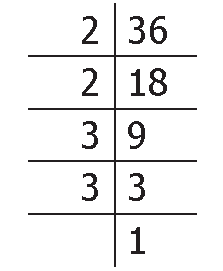36  =  2 x 2 x 3 x 3

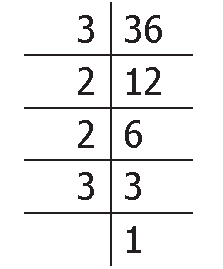36  =  3 x 2 x 2 x 3

In the above method, why do we start with 2 or 3 ? why not with 5 ?

Because, we know that 36 is not a multiple of 5 and hence not divisible by 5. So, to find the prime factors of a number, it will be useful to check for divisibility by smaller numbers like 2, 3 and 5 first and not take numbers at random. 

Factor Tree Method

Using Factor Tree Method, we can find the prime factorization of 36 as follows :

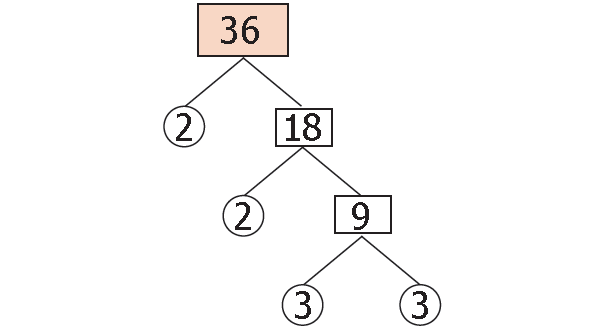
Prime factorization of 36 :

36  =  2 x 2 x 3 x 3

In each step put a prime factor (e.g. 2, 3, 5, 7, 11, 13, etc.) into the CIRCLE and the other factor into the BOX .

In the next step, factor the number in the BOX by putting one of its prime factors into the CIRCLE and the other factor into the BOX.

Continue until you reach a number which has only two prime factors and put each of them into a CIRCLE.

Then, write down all of the  factors in the CIRCLES and that is your prime factorization of the original number.

Solved Problems

Problem 1 :

Find the prime factors  108 by division method. 

Solution : 

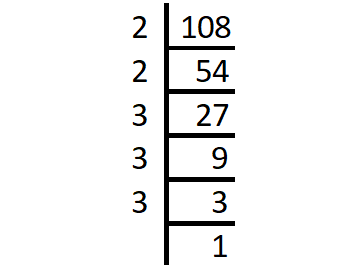
Prime factorization of 108 :

108  =  2 x 2 x 3 x 3 x 3

Problem 2 :

Find the prime factors  144 by division method. 

Solution : 

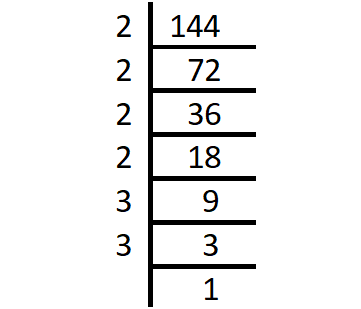
Prime factorization of 144 :

144  =  2 x 2 x 2 x 2 x 3 x 3

Problem 3 : 

Find the prime factors  of 56 by factor tree method. 

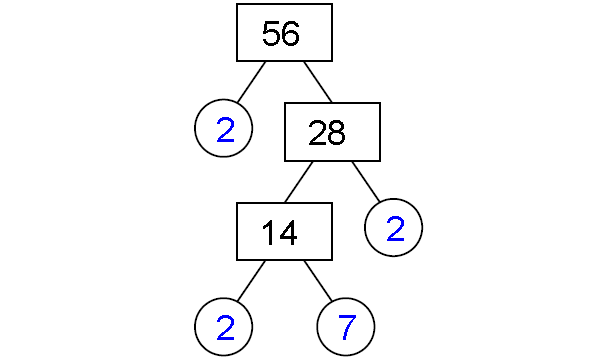
Prime factorization of 56 :

56  =  2 x 2 x 2 x 7

Problem 4 : 

Find the prime factors  of 80 by factor tree method. 

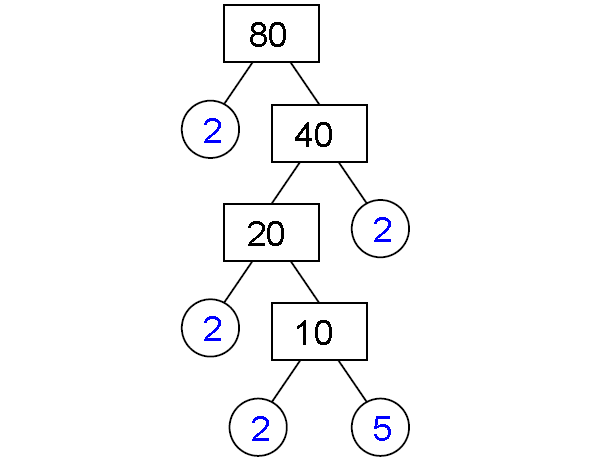
Prime factorization of 80 :

80  =  2 x 2 x 2 x 2 x 5

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.